练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

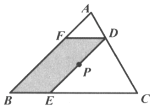
    【题目】如图，已知点P是△ABC的重心，过P作AB的平行线DE,分别交AC于点D,交BC于点E,作DF//BC,交AB于点F,若四边形BEDF的面积为4,则△ABC的面积为__________

    【答案】9

    【解析】

    连接CP交AB于点H,利用点P是重心得到=，得出S△DEC=4S△AFD,再由DE//BF证出，由此得到S△DEC=S△ABC，继而得出S四边形BEDF=S△ABC，从而求出△ABC的面积.

    如图，连接CP交AB于点H,

    ∵点P是△ABC的重心，

    ∴,

    ∴,

    ∵DF//BE,

    ∴△AFD∽△DEC,

    ∴S△DEC=4S△AFD,

    ∵DE//BF,

    ∴,△DEC∽△ABC,

    ∴S△ABC=S△DEC,

    ∴S四边形BEDF=S△ABC,

    ∵四边形BEDF的面积为4,

    ∴S△ABC=9

    故答案为：9.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝2，点F是边BC上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG，CG，则四边形AGCD的面积的最小值为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点，

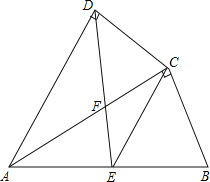
    （1）求证：AC2=ABAD；

    （2）求证：CE∥AD；

    （3）若AD=4，AB=6，求 的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

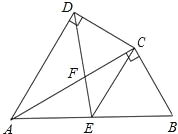
    【题目】如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点，

    （1）求证：AC2＝ABAD；

    （2）求证：△AFD∽△CFE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

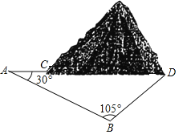
    【题目】2019年11月26日，鲁南高铁正式开通运营．鲁南高铁临沂段修建过程中需要经过一座小山．如图，施工方计划沿AC方向挖隧道，为了加快施工速度，要在小山的另一侧D（A、C、D共线）处同时施工．测得∠CAB＝30°，，∠ABD＝105°，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

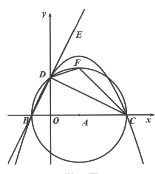
    【题目】如图，已知点B的坐标是（-2，0)，点C的坐标是（8，0)，以线段BC为直径作⊙A，交y轴的正半轴于点D，过B、C、D三点作抛物线.

    （1）求抛物线的解析式；

    （2）连结BD，CD，点E是BD延长线上一点，∠CDE的角平分线DF交⊙A于点F，连结CF，在直线BE上找一点P，使得△PFC的周长最小，并求出此时点P的坐标；

    （3）在（2）的条件下，抛物线上是否存在点G，使得∠GFC=∠DCF，若存在，请直接写出点G的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝﹣2x2+bx+c的图象经过点（0，6）和（1，8）．

    （1）求这个二次函数的解析式；

    （2）①当x在什么范围内时，y随x的增大而增大？

    ②当x在什么范围内时，y＞0？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图,在四边形ABCD中，AD∥BC，AD=2BC, E为AD的中点,连接BD,BE，∠ABD=90°

    （1）求证：四边形BCDE为菱形.

    （2）连接AC,若AC⊥BE, BC=2,求BD的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BD是⊙O的直径．弦AC垂直平分OD，垂足为E．

    （1）求∠DAC的度数；

    （2）若AC＝6，求BE的长．

    查看答案和解析>>

    同步练习册答案