
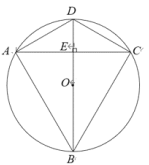
【题目】如图,BD是⊙O的直径.弦AC垂直平分OD,垂足为E.
(1)求∠DAC的度数;
(2)若AC=6,求BE的长.
【答案】(1)30°;(2)3![]()
【解析】
(1)由题意证明△CDE≌△COE,从而得到△OCD是等边三角形,然后利用同弧所对的圆周角等于圆心角的一半求解;(2)由垂径定理求得AE=![]() AC=3,然后利用30°角的正切值求得DE=
AC=3,然后利用30°角的正切值求得DE=![]() ,然后根据题意求得OD=2DE=2
,然后根据题意求得OD=2DE=2![]() ,直径BD=2OD=4
,直径BD=2OD=4![]() ,从而使问题得解.
,从而使问题得解.
解:连接OA,OC
∵弦AC垂直平分OD
∴DE=OE,∠DEC=∠OEC=90°
又∵CE=CE
∴△CDE≌△COE
∴CD=OC
又∵OC=OD
∴CD=OC=OD
∴△OCD是等边三角形
∴∠DOC=60°
∴∠DAC=30°
(2)∵弦AC垂直平分OD
∴AE=![]() AC=3
AC=3
又∵由(1)可知,在Rt△DAE中,∠DAC=30°
∴![]() ,即
,即![]()
∴DE=![]()
∵弦AC垂直平分OD
∴OD=2DE=2![]()
∴直径BD=2OD=4![]()
∴BE=BD-DE=4![]() -
-![]() =3
=3![]()


科目:初中数学 来源: 题型:
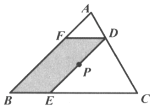
【题目】如图,已知点P是△ABC的重心,过P作AB的平行线DE,分别交AC于点D,交BC于点E,作DF//BC,交AB于点F,若四边形BEDF的面积为4,则△ABC的面积为__________
查看答案和解析>>
科目:初中数学 来源: 题型:
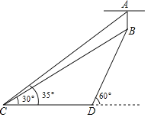
【题目】如图,宾馆大厅的天花板上挂有一盏吊灯AB,某人从C点测得吊灯顶端A的仰角为![]() ,吊灯底端B的仰角为
,吊灯底端B的仰角为![]() ,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为
,从C点沿水平方向前进6米到达点D,测得吊灯底端B的仰角为![]() .请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,
.请根据以上数据求出吊灯AB的长度.(结果精确到0.1米.参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6,AB=10.现分别以点A、点B为圆心,以大于![]() AB相同的长为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若将△BDE沿直线MN翻折得△B′DE,使△B′DE与△ABC落在同一平面内,连接B′E、B′C,则△B′CE的周长为_____.
AB相同的长为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若将△BDE沿直线MN翻折得△B′DE,使△B′DE与△ABC落在同一平面内,连接B′E、B′C,则△B′CE的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学不仅是一门学科,也是一种文化,即数学文化.数学文化包括数学史、数学美和数学应用等多方面.古时候,在某个王国里有一位聪明的大臣,他发明了国际象棋,献给了国王,国王从此迷上了下棋,为了对聪明的大臣表示感谢,国王答应满足这位大臣的一个要求.大臣说:“就在这个棋盘上放一些米粒吧.第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,第
粒米,第![]() 格放
格放![]() 粒米,然后是
粒米,然后是![]() 粒、
粒、![]() 粒、
粒、![]() 粒······一只到第
粒······一只到第![]() 格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求
格.”“你真傻!就要这么一点米粒?”国王哈哈大笑.大臣说:“就怕您的国库里没有这么多米!”国王的国库里真没有这么多米吗?题中问题就是求![]() 是多少?请同学们阅读以下解答过程就知道答案了.
是多少?请同学们阅读以下解答过程就知道答案了.
设![]() ,
,
则![]()
![]()
![]()
即:![]()
事实上,按照这位大臣的要求,放满一个棋盘上的![]() 个格子需要
个格子需要![]() 粒米.那么
粒米.那么![]() 到底多大呢?借助计算机中的计算器进行计算,可知答案是一个
到底多大呢?借助计算机中的计算器进行计算,可知答案是一个![]() 位数:
位数:![]()
![]() ,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
,这是一个非常大的数,所以国王是不能满足大臣的要求.请用你学到的方法解决以下问题:
![]() 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座
我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座![]() 层塔共挂了
层塔共挂了![]() 盏灯,且相邻两层中的下一层灯数是上一层灯数的
盏灯,且相邻两层中的下一层灯数是上一层灯数的![]() 倍,则塔的顶层共有多少盏灯?
倍,则塔的顶层共有多少盏灯?
![]() 计算:
计算: ![]()
![]() 某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
某中学“数学社团”开发了一款应用软件,推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案:
已知一列数:![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,求满足如下条件的所有正整数
,以此类推,求满足如下条件的所有正整数![]() ,且这一数列前
,且这一数列前![]() 项和为
项和为![]() 的正整数幂.请直接写出所有满足条件的软件激活码正整数
的正整数幂.请直接写出所有满足条件的软件激活码正整数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代城市绿化带在不断扩大,绿化用水的节约是一个非常重要的问题.


如图1、图2所示,某喷灌设备由一根高度为0.64 m的水管和一个旋转喷头组成,水管竖直安装在绿化带地面上,旋转喷头安装在水管顶部(水管顶部和旋转喷头口之间的长度、水管在喷灌区域上的占地面积均忽略不计),旋转喷头可以向周围喷出多种抛物线形水柱,从而在绿化带上喷灌出一块圆形区域.现测得喷的最远的水柱在距离水管的水平距离3 m处达到最高,高度为1 m.
(1)求喷灌出的圆形区域的半径;
(2)在边长为16 m的正方形绿化带上固定安装三个该设备,喷灌区域可以完全覆盖该绿化带吗?如果可以,请说明理由;如果不可以,假设水管可以上下调整高度,求水管高度为多少时,喷灌区域恰好可以完全覆盖该绿化带.(以上需要画出示意图,并有必要的计算、推理过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AC和BC为腰向外作等腰直角△DAC和等腰直角△EBC,连接DE.

(1)求证:△DAC∽△EBC;
(2)求△ABC与△DEC的面积比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和
和 ![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式,并写出![]() 点的坐标;
点的坐标;
(2)如图,点![]() 分别在线段
分别在线段![]() 上(
上(![]() 点不与
点不与![]() 重合),且
重合),且![]() ,则
,则![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的长;若不能,请说明理由;
的长;若不能,请说明理由;
(3)若点![]() 在抛物线上,且
在抛物线上,且![]() ,试确定满足条件的点
,试确定满足条件的点![]() 的个数.
的个数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于60元,经市场调查,每天的销售量y(单位:千克)与每千克售价x(单位:元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 45 | 50 | 60 |
销售量y(千克) | 110 | 100 | 80 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为w(单位:元),则当每千克售价x定为多少元时,超市每天能获得的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com