
����Ŀ����ѧ������һ��ѧ�ƣ�Ҳ��һ���Ļ�������ѧ�Ļ�.��ѧ�Ļ�������ѧʷ����ѧ������ѧӦ�õȶ��.��ʱ����ij����������һλ�����Ĵ��������˹������壬���˹����������Ӵ����������壬Ϊ�˶Դ����Ĵ�ʾ��л��������Ӧ������λ��һ��Ҫ��.��˵����������������Ϸ�һЩ������.��![]() ���
���![]() ���ף���
���ף���![]() ���
���![]() ���ף���
���ף���![]() ���
���![]() ���ף�Ȼ����
���ף�Ȼ����![]() ����
����![]() ����
����![]() ��������������һֻ����
��������������һֻ����![]() ��.��������ɵ����Ҫ��ôһ��������������������Ц.��˵�����������Ĺ�����û����ô���ף��������Ĺ�������û����ô�������������������
��.��������ɵ����Ҫ��ôһ��������������������Ц.��˵�����������Ĺ�����û����ô���ף��������Ĺ�������û����ô�������������������![]() �Ƕ��٣���ͬѧ���Ķ����½����̾�֪������.
�Ƕ��٣���ͬѧ���Ķ����½����̾�֪������.
��![]() ,
,
��![]()
![]()
![]()
����![]()
��ʵ�ϣ�������λ��Ҫ����һ�������ϵ�![]() ��������Ҫ
��������Ҫ![]() ����.��ô
����.��ô![]() �������?����������еļ��������м��㣬��֪����һ��
�������?����������еļ��������м��㣬��֪����һ��![]() λ��:
�:![]()
![]() ������һ���dz�����������Թ����Dz��������Ҫ��.������ѧ���ķ��������������:
������һ���dz�����������Թ����Dz��������Ҫ��.������ѧ���ķ��������������:
![]() �ҹ��Ŵ���ѧ�������㷨ͳ�ڡ�������������:��Զ��ΡΡ���߲㣬����㱶�������������ٰ�ʮһ�����ʼ�ͷ��յ��?����˼��:һ��
�ҹ��Ŵ���ѧ�������㷨ͳ�ڡ�������������:��Զ��ΡΡ���߲㣬����㱶�������������ٰ�ʮһ�����ʼ�ͷ��յ��?����˼��:һ��![]() ����������
����������![]() յ�ƣ������������е���һ���������һ�������
յ�ƣ������������е���һ���������һ�������![]() ���������Ķ��㹲�ж���յ��?
���������Ķ��㹲�ж���յ��?
![]() ����:
����: ![]()
![]() ij��ѧ����ѧ������������һ��Ӧ���������Ƴ���������ѧ���ȡ�������������Ļ.��������ļ�����Ϊ������ѧ����Ĵ𰸣�
ij��ѧ����ѧ������������һ��Ӧ���������Ƴ���������ѧ���ȡ�������������Ļ.��������ļ�����Ϊ������ѧ����Ĵ𰸣�
��֪һ������![]() �����е�һ����
�����е�һ����![]() ����������������
����������������![]() ���ٽ�������������
���ٽ�������������![]() ���Դ����ƣ���������������������������
���Դ����ƣ���������������������������![]() ������һ����ǰ
������һ����ǰ![]() ���Ϊ
���Ϊ![]() ����������.��ֱ��д��������������������������������
����������.��ֱ��д��������������������������������![]() ��ֵ.
��ֵ.
���𰸡���1��3����2��![]() ����3��
����3��![]()
��������
![]() �����Ķ��㹲��
�����Ķ��㹲��![]() յ�ƣ����������г����̣����н��.
յ�ƣ����������г����̣����н��.
![]() ������Ŀ�еĽ��ⷽ�����м��㼴��.
������Ŀ�еĽ��ⷽ�����м��㼴��.
![]() ������������е�ÿһ���ǰn���Sn=2n+1-2-n�����������������֪��2n+1Ϊ2�������ݣ�ֻ�轫-2-n��ȥ���ɣ��ֱ�ֱ����N��ֵ
������������е�ÿһ���ǰn���Sn=2n+1-2-n�����������������֪��2n+1Ϊ2�������ݣ�ֻ�轫-2-n��ȥ���ɣ��ֱ�ֱ����N��ֵ
![]() �����Ķ��㹲��
�����Ķ��㹲��![]() յ�ƣ��������
յ�ƣ��������
![]() .
.
���![]() ��
��
![]() ���㹲��
���㹲��![]() յ��.
յ��.
![]() ��
��![]() ,
,
![]()
![]() ,
,
����![]()
![]() .
.
��![]()
![]() �������֪��20��һ��,20,21�ڶ���,20,21,22������,��20,21,22��,2n1��n�
�������֪��20��һ��,20,21�ڶ���,20,21,22������,��20,21,22��,2n1��n�
���ݵȱ�����ǰn���ʽ,���ÿ��ͷֱ�Ϊ��![]()
ÿ��е�����Ϊ��1��2��3������n��
�ܹ�������Ϊ![]()
���������ĺ�Ϊ![]()
![]()
![]()
![]()
�������֪��![]() Ϊ2�������ݣ�ֻ�轫2n��ȥ���ɣ�
Ϊ2�������ݣ�ֻ�轫2n��ȥ���ɣ�
���1+2+(2n)=0,��ã�n=1,�ܹ���![]() ��������N>10��
��������N>10��
��1+2+4+(2n)=0,��ã�n=5,�ܹ���![]() ����
����![]() ��
��
��1+2+4+8+(2n)=0,��ã�n=13,�ܹ���![]() ����
����![]() ��
��
��1+2+4+8+16+(2n)=0,��ã�n=29,�ܹ���![]() ������
������![]() ��
��
��![]()


 �ִʾ��ƪϵ�д�
�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ������һ��A��B���ͺŽ��ܵƣ���֪2ֻA�ͽ��ܵƺ�3ֻB�ͽ��ܵƹ���31Ԫ��1ֻA�ͽ��ܵƺ�2ֻB�ͽ��ܵƹ���19Ԫ��
��1����һֻA�ͽ��ܵƺ�һֻB�ͽ��ܵƵ��ۼ۸��Ƕ���Ԫ��
��2��ѧУ�������������ͺŵĽ��ܵƹ�100ֻ������A�ͽ��ܵƵ�����������B�ͽ��ܵ�������2��������Ƴ���ʡǮ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ�Ľ���Ϊÿ��40Ԫ���ۼ�Ϊÿ��50Ԫ��ÿ���¿�����200�������ÿ����Ʒ���ۼ�ÿ����2Ԫ����ÿ��������5������ÿ����Ʒ���ۼ�ΪxԪ�������y����ÿ������������ΪwԪ��
��1����y��x�ĺ�����ϵʽ��
��2��ÿ����Ʒ���ۼ۶�Ϊ����Ԫʱ��ÿ���¿ɻ��������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
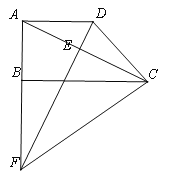
����Ŀ����ͼ����֪����ABCD�У�AD//BC ����ABC=90����BC=2AB=8���Խ���ACƽ�֡�BCD������D��DE��AC������Ϊ��E������AB���ӳ����ڵ�F������CF��
��1������DC�ij���
��2�����BCF������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
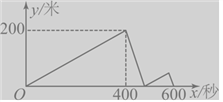
����Ŀ���ס���������ͬһֱ�߇�·��ͬ��㣬ͬ����ͬ���������ֱ��Բ�ͬ���ٶ������ܲ�1500�ף����׳�����200��ʱ����ͣ�����Ⱥ��ң��ס��һ�Ϻ����˷ֱ���ԭ�����ٶȼ��������յ㣬�ȵ����յ�������յ���Ϣ�����ܲ������������У��ס������˵ľ���y���ף��������ʱ��x���룩֮��Ĺ�ϵ��ͼ��ʾ������յ�ʱ���Ҿ����յ�______________�ס�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڡ�ABC�У�AB=AC�� ��1������A=36���ڡ�ABC�л�һ���߶Σ��ܵõ�2�����������Σ���������ABC������2�����������εĶ��ǵĶ����ֱ���_____����2������A��36�� ����A=_____ʱ���ڵ�����ABC�л�һ���߶Σ��ܵõ�2�����������Σ���������ABC��.��д�������𰸼��ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x�ķ��̣�2m+1��x2+4mx+2m��3��0����������ȵ�ʵ������
��1����m��ȡֵ��Χ��
��2���Ƿ����ʵ��m��ʹ���̵�����ʵ�����ĵ���֮�͵��ک�1�������ڣ����m��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
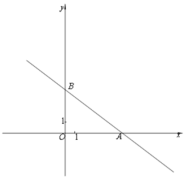
����Ŀ����ƽ��ֱ������ϵ![]() �У�ֱ��
�У�ֱ��![]()
![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�A��B��ͼ��ʾ����
��ֱ��ڵ�A��B��ͼ��ʾ����![]() ���߶�
���߶�![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ��
��
��1���ú���ĸ![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() �����ꣻ
�����ꣻ
��2��������y������![]() ��
��![]() ����������ߵı���ʽ��
����������ߵı���ʽ��
��3���ڵڣ�2����������£�λ�ڵ��������������ϣ��Ƿ���������ĵ�![]() ��ʹ
��ʹ![]() ��������ڣ������
��������ڣ������![]() �����꣬��������ڣ���˵�����ɣ�
�����꣬��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
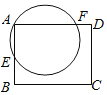
����Ŀ����ͼ���ھ���ABCD�У�����A��ԲO����AB�ڵ�E������AD�ڵ�F����֪AD=5��AE=2��AF=4������Ե�DΪԲ�ģ�rΪ�뾶��ԲD��ԲO�����������㣬��ôr��ȡֵ��Χ��______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com