已知=x2+mx+n.则m+n=-3．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

13．已知（x+1）（x-2）=x²+mx+n，则m+n=-3．

分析已知等式左边利用多项式乘以多项式法则计算，再利用多项式相等的条件求出m与n的值，即可求出m+n的值．

解答解：已知等式变形得：x²-x-2=x²+mx+n，
可得m=-1，n=-2，
则m+n=-1-2=-3．
故答案为：-3

点评此题考查了多项式乘多项式，熟练掌握运算法则是解本题的关键．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

3．

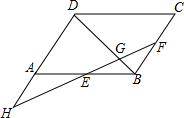如图所示，在?ABCD中，E为AB中点，在BC上取一点F，使BF：FC=1：2，连接EF交DA的延长线于H，交BD于G．试说明：BD=5BG．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

4．下列调查中，适宜采用全面调查方式的是（　　）

	A．	调查春节联欢晚会在武汉市的收视率
	B．	了解全班同学参加社会实践活动的情况
	C．	调查某品牌食品的色素含量是否达标
	D．	了解一批手机电池的使用寿命

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

1．

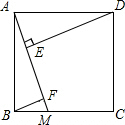如图，正方形ABCD的边长为5，点M是边BC上的点，DE⊥AM于点E，BF∥DE，交AM于点F．若E是AF的中点，则DE的长为（　　）

A．

$\sqrt{5}$

B．

2$\sqrt{5}$

C．

D．

2$\sqrt{3}$

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

8．数1，$\frac{3}{4}$，$\frac{5}{9}$，$\frac{7}{16}$，$\frac{9}{25}$…按此规律写下去，那么第n（n为正整数）个数是（　　）

A．

$\frac{2n+1}{{n}^{2}}$

B．

$\frac{2n-1}{n}$

C．

$\frac{2n-1}{{n}^{2}}$

D．

$\frac{n-4}{{n}^{2}}$

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

18．已知$\frac{|x|}{x-2}$=$\frac{x}{2-x}$，则x一定满足（　　）

A．

x＜2

B．

x≤0

C．

x≥0

D．

x≥0且x≠2

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

5．（1）$\frac{b}{a}$-$\frac{b+1}{a}$
（2）$\frac{{x}^{2}+xy}{xy}$-$\frac{{x}^{2}-xy}{xy}$
（3）$\frac{（{a-2b）}^{2}}{ab}$-$\frac{（a+2b）^{2}}{ab}$
（4）$\frac{{x}^{2}-y}{（x-3）^{2}}$-$\frac{9-y}{（3-x）^{2}}$　　　　
（5）$\frac{{a}^{2}-1}{{a}^{2}-2a}$+$\frac{4a-5}{2a-{a}^{2}}$
（6）$\frac{12}{{m}^{2}-9}$-$\frac{2}{m-2}$
（7）$\frac{{x}^{2}+9x}{{x}^{2}+3x}$+$\frac{{x}^{2}-9}{{x}^{2}+6x+9}$
（8）$\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$
（9）$\frac{{x}^{2}}{x-1}$-x-1．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

2．