
【题目】阅读下面材料:点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.回答下列问题:
(1)数轴上表示﹣3和1两点之间的距离是 ,数轴上表示﹣2和3的两点之间的距离是 ;
(2)数轴上表示x和﹣1的两点之间的距离表示为 ;
(3)若x表示一个有理数,则|x﹣2|+|x+3|有最小值吗?若有,请求出最小值;若没有,请说明理由.
![]()
【答案】(1)4,5;(2)|x+1|;(3)5.
【解析】
(1)根据在数轴上A、B两点之间的距离为AB=|a﹣b|即可求解;
(2)根据在数轴上A、B两点之间的距离为AB=|a﹣b|即可求解;
(3)根据绝对值的性质去掉绝对值号,然后计算即可得解.
(1)|1﹣(﹣3)|=4;|3﹣(﹣2)|=5;
故答案为:4;5;
(2)|x﹣(﹣1)|=|x+1|或|(﹣1)﹣x|=|x+1|,
故答案为:|x+1|;
(3)有最小值,
当x<﹣3时,|x﹣2|+|x+3|=2﹣x﹣x﹣3=﹣2x﹣1,
当﹣3≤x≤2时,|x﹣2|+|x+3|=2﹣x+x+3=5,
当x>2时,|x﹣2|+|x+3|=x﹣2+x+3=2x+1,
在数轴上|x﹣2|+|x+3|的几何意义是:表示有理数x的点到﹣3及到2的距离之和,所以当﹣3≤x≤2时,它的最小值为5.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】威丽商场销售A、B两种商品,售出1件A种商品和4件B种商品所得利润为600元;售出3件A种商品和5件B种商品所得利润为1100元.
(1)求每件A种商品和每件B种商品售出后所得利润分别为多少元?
(2)由于需求量大,A、B两种商品很快售完,威丽商场决定再一次购进A、B两种商品共34件,如果将这34件商品全部售完后所得利润不低于4000元,那么威丽商场至少需购进多少件A种商品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,![]() 是函数
是函数![]() 的图像上一点,
的图像上一点,![]() 是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
(1)求a的值;
(2)如图②,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若点P也在函数![]() 的图像上,求b的值;
的图像上,求b的值;
(4)设正方形ABPQ的中心为M,点N是函数![]() 的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
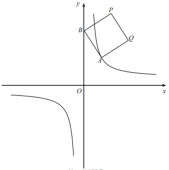
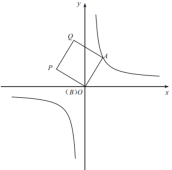

图① 图② 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在△ABC中,AB=3,AD=6,问△ABC的高AD与CE的比是多少?
小聪的计算思路是:
根据题意得:S△ABC=![]() BCAD=
BCAD=![]() ABCE.
ABCE.
从而得2AD=CE,∴![]()
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在ABCD中,点E、F分别在AD,CD上,且AF=CE,并相交于点O,连接BE、BF,
求证:BO平分角AOC.
(2)【探究延伸】
如图3,已知直线m∥n,点A、C是直线m上两点,点B、D是直线n上两点,点P是线段CD中点,且∠APB=90°,两平行线m、n间的距离为4.求证:PAPB=2AB.
(3)【迁移应用】
如图4,E为AB边上一点,ED⊥AD,CE⊥CB,垂足分别为D,C,∠DAB=∠B,AB=![]() ,BC=2,AC=
,BC=2,AC=![]() ,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
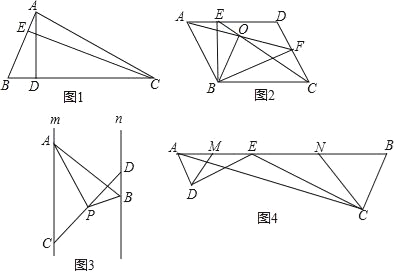
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个正方形ABCD,点P是边BC上一点.将![]() 绕点A逆时针方向旋转90°得到
绕点A逆时针方向旋转90°得到![]() (点B,P的对应点分别是
(点B,P的对应点分别是![]() )
)
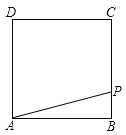
(1)画出旋转后所得到的![]() ;
;
(2)联结![]() ,设
,设![]() ,
,![]() ,试用
,试用![]() 表示
表示![]() 的面积;
的面积;
(3)若![]() 的面积为18,
的面积为18,![]() 的面积为5,试求PC的长.
的面积为5,试求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
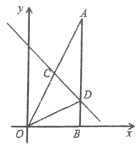
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,直线y=-x+b分别交OA、AB于点C、D,且ΔBOD的面积是4.
(1)求直线AO的解析式;
(2)求直线CD的解析式;
(3)若点M是x轴上的点,且使得点M到点A和点C的距离之和最小,求点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com