
����Ŀ���������龰�����������ε������������ķ�����һ�ֳ����ĵȻ������˷��������ǽ�����������;��֮һ��
���磺����ʦ��С���������һ�����⣺
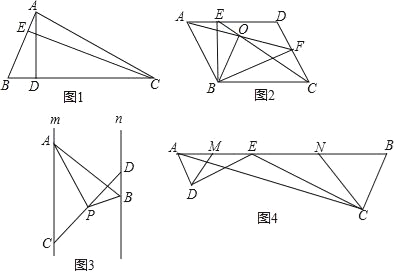
��ͼ1������ABC�У�AB=3��AD=6������ABC�ĸ�AD��CE�ı��Ƕ��٣�
С�ϵļ���˼·�ǣ�
��������ã�S��ABC=![]() BCAD=
BCAD=![]() ABCE��
ABCE��
�Ӷ���2AD=CE����![]()
���������������������۵ľ���ͷ�������������⣺
��1�������̽����
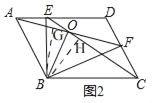
��ͼ2����ABCD�У���E��F�ֱ���AD��CD�ϣ���AF=CE�����ཻ�ڵ�O������BE��BF��
��֤��BOƽ�ֽ�AOC��
��2����̽�����졿
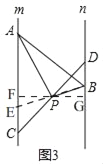
��ͼ3����ֱ֪��m��n����A��C��ֱ��m�����㣬��B��D��ֱ��n�����㣬��P���߶�CD�е㣬�ҡ�APB=90������ƽ����m��n��ľ���Ϊ4����֤��PAPB=2AB��
��3����Ǩ��Ӧ�á�
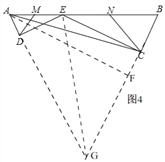
��ͼ4��EΪAB����һ�㣬ED��AD��CE��CB������ֱ�ΪD��C����DAB=��B��AB=![]() ��BC=2��AC=
��BC=2��AC=![]() ������֪M��N�ֱ�ΪAE��BE���е㣬����DM��CN������DEM����CEN���ܳ�֮�ͣ�
������֪M��N�ֱ�ΪAE��BE���е㣬����DM��CN������DEM����CEN���ܳ�֮�ͣ�
���𰸡���1������������2������������3��5+![]()
��������������(1)������ƽ���ı��ε����ʵó���ABF�͡�BCE�������ȣ�����B��OG��AF��G��OH��CE��H���Ӷ��ó�AF=CE��Ȼ��֤����BOG�͡�BOHȫ�ȣ��Ӷ��ó���BOG=��BOH������ƽ���ߣ�(2)������P��PG��n��G����m��F������ƽ���ߵ����ʵó���CPF����DPGȫ�ȣ��ӳ�BP��AC��E��֤����CPE�͡�DPBȫ�������ݵȻ����ó�AB=![]() AP��PB���Ӷ��ó��𰸣�(3)�����ӳ�AD��BC���ڵ�G������A��AF��BC��F����CF=x������Rt��ABF��Rt��ACF�Ĺ��ɶ����ó�x��ֵ�����ݵȻ����ó�AE=2DM=2EM��BE=2CN=2EN�� DM+CN=
AP��PB���Ӷ��ó��𰸣�(3)�����ӳ�AD��BC���ڵ�G������A��AF��BC��F����CF=x������Rt��ABF��Rt��ACF�Ĺ��ɶ����ó�x��ֵ�����ݵȻ����ó�AE=2DM=2EM��BE=2CN=2EN�� DM+CN=![]() AB���Ӷ��ó����������ε��ܳ�֮�ͣ�
AB���Ӷ��ó����������ε��ܳ�֮�ͣ�
ͬ����EM+EN=![]() AB
AB
��⣺֤������1����ͼ2�� ���ı���ABCD��ƽ���ı��Σ�
��S��ABF=![]() SABCD��S��BCE=
SABCD��S��BCE=![]() SABCD�� ��S��ABF=S��BCE��
SABCD�� ��S��ABF=S��BCE��
����B��OG��AF��G��OH��CE��H�� ��S��ABF=![]() AF��BG��S��BCE=
AF��BG��S��BCE=![]() CE��BH��
CE��BH��
��![]() AF��BG=
AF��BG=![]() CE��BH������AF��BG=CE��BH�� ��AF=CE�� ��BG=BH��
CE��BH������AF��BG=CE��BH�� ��AF=CE�� ��BG=BH��
��Rt��BOG��Rt��BOH��![]() �� ��Rt��BOG��Rt��BOH�� ���BOG=��BOH��
�� ��Rt��BOG��Rt��BOH�� ���BOG=��BOH��
��OBƽ�֡�AOC��
��2����ͼ3������P��PG��n��G����m��F�� ��m��n�� ��PF��AC��
���CFP=��BGP=90�㣬 �ߵ�P��CD�е㣬
����CPF����DPG�У� �� ���CPF�ա�DPG�� ��PF=PG=
�� ���CPF�ա�DPG�� ��PF=PG=![]() FG=2��
FG=2��
�ӳ�BP��AC��E�� ��m��n�� ���ECP=��BDP�� ��CP=DP��
����CPE����DPB�У� �� ���CPE�ա�DPB�� ��PE=PB��
�� ���CPE�ա�DPB�� ��PE=PB��
�ߡ�APB=90�㣬 ��AE=AB�� ��S��APE=S��APB��
��S��APE=![]() AE��PF=AE=AB��S��APB=
AE��PF=AE=AB��S��APB=![]() AP��PB��
AP��PB��
��AB=![]() AP��PB�� ����PAPB=2AB��
AP��PB�� ����PAPB=2AB��
��3����ͼ4���ӳ�AD��BC���ڵ�G�� �ߡ�BAD=��B��
��AG=BG������A��AF��BC��F��
��CF=x��x��0���� ��BF=BC+CF=x+2�� ��Rt��ABF��AB=![]() ��
��
���ݹ��ɶ����ã�AF2=AB2��BF2=34����x+2��2�� ��Rt��ACF�У�AC=![]() ��
��
���ݹ��ɶ����ã�AF2=AC2��CF2=26��x2��
��34����x+2��2=26��x2�� ��x=��1���ᣩ��x=1�� ��AF=![]() =5��
=5��
����EG�� ��S��ABG=![]() BG��AF=S��AEG+S��BEG=
BG��AF=S��AEG+S��BEG=![]() AG��DE+
AG��DE+![]() BG��CE=
BG��CE=![]() BG��DE+CE����
BG��DE+CE����
��DE+CE=AF=5�� ��Rt��ADE�У���M��AE���е㣬 ��AE=2DM=2EM��
ͬ����BE=2CN=2EN�� ��AB=AE+BE�� ��2DM+2CN=AB�� ��DM+CN=![]() AB��
AB��
ͬ����EM+EN=![]() AB ���DEM����CEN���ܳ�֮��=DE+DM+EM+CE+CN+EN=��DE+CE��+[��DM+CN��+��EM+EN��]
AB ���DEM����CEN���ܳ�֮��=DE+DM+EM+CE+CN+EN=��DE+CE��+[��DM+CN��+��EM+EN��]
=��DE+CN��+AB=5+![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�AB��20����C��BA���ӳ����ϣ���D��ֱ��AB�ϣ�AC��12��BD��16����M���߶�CD���е㣬��AM�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ƻ���900Ԫ���������ҹ���50̨����������֪�ó����������ֲ�ͬ�ͺŵļ������������۷ֱ�ΪA��ÿ̨15Ԫ��B��ÿ̨21Ԫ��C�֚�̨25Ԫ��
��1���̳�ͬʱ�������ֲ�ͬ�ͺŵļ�����50̨����ȥ900Ԫ��
����ͬʱ����A��B ����ʱ����A��B ���ּ�����������̨����
����ͬʱ����A��C ����ʱ����A��C ���ּ�����������̨����
��2�����̳�����һ̨A�ּ������ɻ���5Ԫ������һ̨B�ּ������ɻ���8Ԫ������һ̨C�ּ������ɻ���12Ԫ����ͬʱ�������ֲ�ͬ�ͺŵļ����������У�Ϊ��ʹ����ʱ������࣬��ѡ�����ַ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̷��������г���ÿ��![]() Ԫ�ļ۸����ֲ�Ҷ40������ÿ��
Ԫ�ļ۸����ֲ�Ҷ40������ÿ��![]() Ԫ�ļ۸����ֲ�Ҷ60��.
Ԫ�ļ۸����ֲ�Ҷ60��.
��1�����̷������ס������ֲ�Ҷ�����ʽ�______Ԫ���ú�![]() ��
��![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��2�������̷������ֲ�Ҷ�����![]() ȫ���۳������ɻ�������Ԫ���ú�
ȫ���۳������ɻ�������Ԫ���ú�![]() ��
��![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
��3�������̷������ֲ�Ҷ����ÿ��![]() Ԫ�ļ۸�ȫ�����ۣ�����������и��̷���ӯ�����ǿ�����˵������.
Ԫ�ļ۸�ȫ�����ۣ�����������и��̷���ӯ�����ǿ�����˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ���A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB��|a��b|���ش��������⣺
��1�������ϱ�ʾ��3��1����֮��ľ������� ���������ϱ�ʾ��2��3������֮��ľ������� ����
��2�������ϱ�ʾx�ͩ�1������֮��ľ����ʾΪ�� ����
��3����x��ʾһ������������|x��2|+|x+3|����Сֵ�����У��������Сֵ����û�У���˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ����
����![]() ��AB���ϵĵ�D˳ʱ����ת
��AB���ϵĵ�D˳ʱ����ת![]() �õ�
�õ�![]() ��AB�ڵ�E����
��AB�ڵ�E����![]() ����
����![]() �������
�������![]()
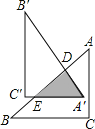
A. 3 B. 5 C. 11 D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ȤС��Ϊ���˽ⱾУ�����μӿ���������������������ȡ��У300�������������ʾ����飬ͳ�����������������������в�������ͳ��ͼ��
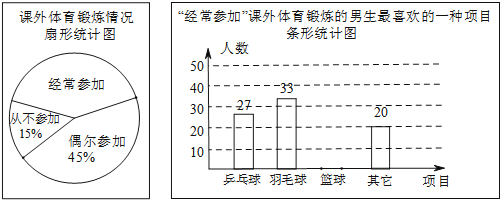
�����������Ϣ����������⣺
![]() �������������������ͳ��ͼ�У��������μ�������Ӧ��Բ�ĽǵĶ���Ϊ______��
�������������������ͳ��ͼ�У��������μ�������Ӧ��Բ�ĽǵĶ���Ϊ______��
![]() �벹ȫ����ͳ��ͼ��
�벹ȫ����ͳ��ͼ��
![]() ��У����1200�������������ȫУ�����о����μӿ�����������������ϲ������Ŀ�������������
��У����1200�������������ȫУ�����о����μӿ�����������������ϲ������Ŀ�������������
![]() С����Ϊ��ȫУ���������У�������ϲ���μӵ��˶���Ŀ��ƹ���������ԼΪ
С����Ϊ��ȫУ���������У�������ϲ���μӵ��˶���Ŀ��ƹ���������ԼΪ![]() ���������ж�����˵���Ƿ���ȷ����˵�����ɣ�
���������ж�����˵���Ƿ���ȷ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
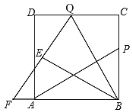
����Ŀ����ͼ��PΪ�߳�Ϊ6��������ABCD�ı�BC��һ����(P��B��C���غ�)��Q��CD�ϣ���CQ=BP������AP��BQ������BQC��BQ���ڵ�ֱ�߷��۵õ���BQE���ӳ�QE��BA���ӳ����ڵ�F.
(1)��̽��AP��BQ��������λ�ù�ϵ����֤����Ľ��ۣ�
(2)��E��FQ���е�ʱ����BP�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����OΪֱ��AB��һ�㣬��ֱ��ABͬ����������OC��OD��ʹ�á�COD=90��
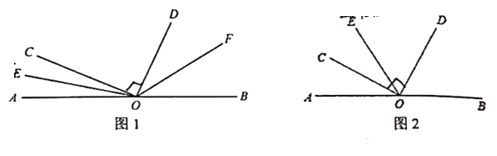
��1����ͼ1������O������OE����OEǡ��Ϊ��AOC�Ľ�ƽ����ʱ����������OF��ʹ��OFƽ�֡�BOD�����EOF�Ķ�����__________�ȣ�
��2����ͼ2������O������OE����OEǡ��Ϊ��AOD�Ľ�ƽ����ʱ�������BOD���COE��������ϵ��
��3������O������OE����OCǡ��Ϊ��AOE�Ľ�ƽ����ʱ����������OF��ʹ��OFƽ�֡�COD������EOC=3��EOF��ֱ��д����AOE�Ķ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com