
【题目】某商场计划用900元从生产厂家购进50台计算器,已知该厂家生产三种不同型号的计算器,出厂价分别为A种每台15元,B种每台21元,C种毎台25元.
(1)商场同时购进两种不同型号的计算器50台,用去900元.
①若同时购进A、B 两种时,则购进A、B 两种计算器各多少台?;
②若同时购进A、C 两种时,则购进A、C 两种计算器各多少台?;
(2)若商场销售一台A种计算器可获利5元,销售一台B种计算器可获利8元,销售一台C种计算器可获利12元,在同时购进两种不同型号的计算器方案中,为了使销售时获利最多,你选择哪种方案?
【答案】(1)①购进![]() 种计算器25台,
种计算器25台,![]() 种计算器25台;②购进
种计算器25台;②购进![]() 种计算器35台,
种计算器35台,![]() 种计算器15台.(2)选择购进
种计算器15台.(2)选择购进![]() 、
、![]() 两种型号的计算器,销售时获利最多.
两种型号的计算器,销售时获利最多.
【解析】
(1)①设购进![]() 种计算器
种计算器![]() 台,则购进
台,则购进![]() 种计算器(
种计算器(![]() 台,根据总钱数=购进
台,根据总钱数=购进![]() 种计算机的钱数+购进
种计算机的钱数+购进![]() 种计算机的钱数即可列出关于x的一元一次方程,解之即可得出结论;
种计算机的钱数即可列出关于x的一元一次方程,解之即可得出结论;
②设购进![]() 种计算器
种计算器![]() 台,则购进
台,则购进![]() 种计算器
种计算器![]() 台,根据总钱数=购进
台,根据总钱数=购进![]() 种计算机的钱数+购进
种计算机的钱数+购进![]() 种计算机的钱数即可列出关于
种计算机的钱数即可列出关于![]() 的一元一次方程,解之即可得出结论;
的一元一次方程,解之即可得出结论;
(2)当只购进![]() 、
、![]() 两种型号时,设购进
两种型号时,设购进![]() 种计算器
种计算器![]() 台,则购进
台,则购进![]() 种计算器
种计算器![]() 台,根据总钱数=购进
台,根据总钱数=购进![]() 种计算机的钱数+购进
种计算机的钱数+购进![]() 种计算机的钱数即可列出关于
种计算机的钱数即可列出关于![]() 的一元一次方程,解之即可得出
的一元一次方程,解之即可得出![]() 的值,从而得出此种进货方式不合理;当只购进
的值,从而得出此种进货方式不合理;当只购进![]() 、
、![]() 两种型号时,根据总利润=销售
两种型号时,根据总利润=销售![]() 种计算器的利润+销售
种计算器的利润+销售![]() 种计算器的利润即可算出选此方案时的利润;当只购进
种计算器的利润即可算出选此方案时的利润;当只购进![]() 、
、![]() 两种型号时,根据总利润=销售
两种型号时,根据总利润=销售![]() 种计算器的利润+销售
种计算器的利润+销售![]() 种计算器的利润即可算出选此方案时的利润.二者比较后即可得出结论.
种计算器的利润即可算出选此方案时的利润.二者比较后即可得出结论.
(1)①设购进![]() 种计算器
种计算器![]() 台,则购进
台,则购进![]() 种计算器(
种计算器(![]() 台,
台,
根据题意得:![]() (
(![]() ,
,
解得:![]() .
.
答:购进![]() 种计算器25台,
种计算器25台,![]() 种计算器25台.
种计算器25台.
②设购进![]() 种计算器
种计算器![]() 台,则购进
台,则购进![]() 种计算器
种计算器![]() 台,
台,
根据题意得:![]() ,
,
解得:![]() .
.
答:购进![]() 种计算器35台,
种计算器35台,![]() 种计算器15台.
种计算器15台.
(2)当只购进![]() 、
、![]() 两种型号时,
两种型号时,
设购进![]() 种计算器
种计算器![]() 台,则购进
台,则购进![]() 种计算器
种计算器![]() 台,
台,
根据题意得:![]() ,
,
解得:![]() (不合题意,舍去).
(不合题意,舍去).
当只购进![]() 、
、![]() 两种型号时,
两种型号时,
利润![]() (元);
(元);
当只购进![]() 、
、![]() 两种型号时,
两种型号时,
利润![]() (元).
(元).
∵![]() ,
,
∴选择购进![]() 、
、![]() 两种型号的计算器,销售时获利最多.
两种型号的计算器,销售时获利最多.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
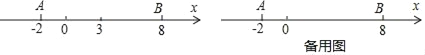
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知P(1,2).
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠B=30°,以A为圆心适当长为半径画弧,分别交AC、AB于点M、N,分别以点M、N为圆心,大于![]() MN的长为半径画弧交于点P,作射线AP交BC于点D,再作射线DE交AB于点E,则下列结论错误的是( )
MN的长为半径画弧交于点P,作射线AP交BC于点D,再作射线DE交AB于点E,则下列结论错误的是( )
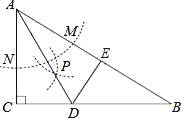
A. ∠ADB=120° B. S△ADC:S△ABC=1:3
C. 若CD=2,则BD=4 D. DE垂直平分AB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,![]() 是函数
是函数![]() 的图像上一点,
的图像上一点,![]() 是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
(1)求a的值;
(2)如图②,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若点P也在函数![]() 的图像上,求b的值;
的图像上,求b的值;
(4)设正方形ABPQ的中心为M,点N是函数![]() 的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
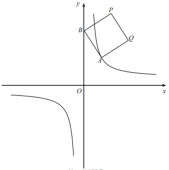
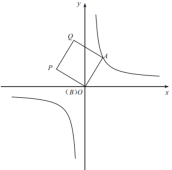

图① 图② 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在△ABC中,AB=3,AD=6,问△ABC的高AD与CE的比是多少?
小聪的计算思路是:
根据题意得:S△ABC=![]() BCAD=
BCAD=![]() ABCE.
ABCE.
从而得2AD=CE,∴![]()
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在ABCD中,点E、F分别在AD,CD上,且AF=CE,并相交于点O,连接BE、BF,
求证:BO平分角AOC.
(2)【探究延伸】
如图3,已知直线m∥n,点A、C是直线m上两点,点B、D是直线n上两点,点P是线段CD中点,且∠APB=90°,两平行线m、n间的距离为4.求证:PAPB=2AB.
(3)【迁移应用】
如图4,E为AB边上一点,ED⊥AD,CE⊥CB,垂足分别为D,C,∠DAB=∠B,AB=![]() ,BC=2,AC=
,BC=2,AC=![]() ,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
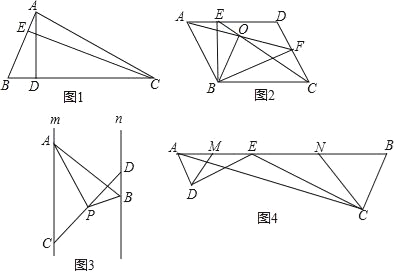
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com