
【题目】求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?

【答案】学校需要投入9000元资金买草皮.
【解析】
仔细分析题目,需要求得四边形的面积才能求得结果.连接BD,在直角三角形ABD中可求得BD的长,由BD、CD、BC的长度关系可得三角形DBC为一直角三角形,DC为斜边;由此看,四边形ABCD由Rt△ABD和Rt△DBC构成,则容易求解.
连接BD,
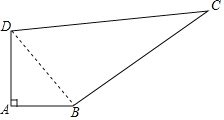
在Rt△ABD中,BD2=AB2+AD2=32+42=52,
在△CBD中,CD2=132,BC2=122,
而122+52=132,
即BC2+BD2=CD2,
∴∠DBC=90°,
S四边形ABCD=S△BAD+S△DBC=![]() ADAB+
ADAB+![]() DBBC,
DBBC,
=![]() ×4×3+
×4×3+![]() ×12×5=36.
×12×5=36.
所以需费用36×250=9000(元),
答:学校需要投入9000元资金买草皮.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商场计划用900元从生产厂家购进50台计算器,已知该厂家生产三种不同型号的计算器,出厂价分别为A种每台15元,B种每台21元,C种毎台25元.
(1)商场同时购进两种不同型号的计算器50台,用去900元.
①若同时购进A、B 两种时,则购进A、B 两种计算器各多少台?;
②若同时购进A、C 两种时,则购进A、C 两种计算器各多少台?;
(2)若商场销售一台A种计算器可获利5元,销售一台B种计算器可获利8元,销售一台C种计算器可获利12元,在同时购进两种不同型号的计算器方案中,为了使销售时获利最多,你选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.
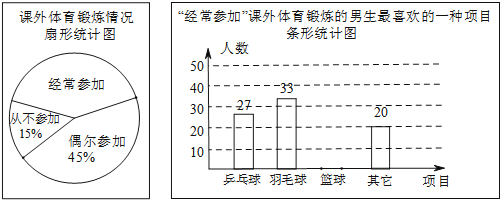
请根据以上信息解答下列问题:
![]() 课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为______;
课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为______;
![]() 请补全条形统计图;
请补全条形统计图;
![]() 该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
![]() 小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为
小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为![]() ”,请你判断这种说法是否正确,并说明理由.
”,请你判断这种说法是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
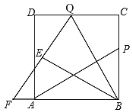
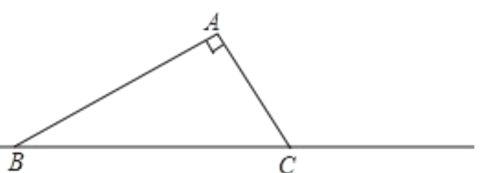
【题目】如图,P为边长为6的正方形ABCD的边BC上一动点(P与B、C不重合),Q在CD上,且CQ=BP,连接AP、BQ,将△BQC沿BQ所在的直线翻折得到△BQE,延长QE交BA的延长线于点F.
(1)试探究AP与BQ的数量与位置关系,并证明你的结论;
(2)当E是FQ的中点时,求BP的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
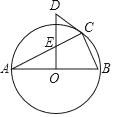
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在△ABC中,AC=3,BC=6,∠C=60![]() ;
;
(1)将△ABC绕着点C旋转,使点A落在直线BC上的点A′,点B落在B′,在下图中画出旋转后的△A′B′C.
(2)直接写出A′B的长,A′B=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
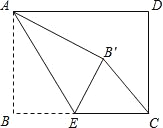
【题目】矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A. 3 B. ![]() C. 2或3 D. 3或
C. 2或3 D. 3或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,在直线AB同侧任作射线OC、OD,使得∠COD=90°
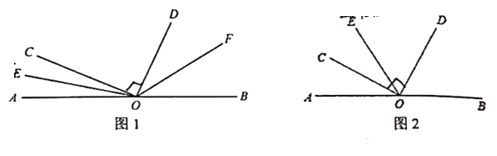
(1)如图1,过点O作射线OE,当OE恰好为∠AOC的角平分线时,另作射线OF,使得OF平分∠BOD,则∠EOF的度数是__________度;
(2)如图2,过点O作射线OE,当OE恰好为∠AOD的角平分线时,求出∠BOD与∠COE的数量关系;
(3)过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,若∠EOC=3∠EOF,直接写出∠AOE的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
月均用水量(单位:t) | 频数 | 百分比 |
2≤x<3 | 2 | 4% |
3≤x<4 | 12 | 24% |
4≤x<5 |
|
|
5≤x<6 | 10 | 20% |
6≤x<7 |
| 12% |
7≤x<8 | 3 | 6% |
8≤x<9 | 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你估计总体小王所居住的小区中等用水量家庭大约有多少户?
(3)从月均用水量在2≤x<3,8≤x<9这两个范围内的样本家庭中任意抽取2个,请用列举法(画树状图或列表)求抽取出的2个家庭来自不同范围的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com