
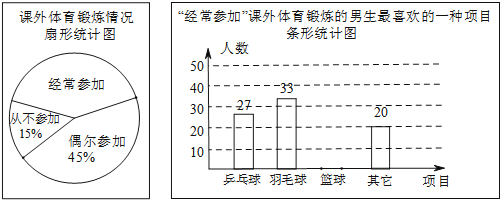
【题目】某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.
请根据以上信息解答下列问题:
![]() 课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为______;
课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为______;
![]() 请补全条形统计图;
请补全条形统计图;
![]() 该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
![]() 小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为
小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为![]() ”,请你判断这种说法是否正确,并说明理由.
”,请你判断这种说法是否正确,并说明理由.
【答案】![]() ;
;![]() 补图见解析;
补图见解析;![]() 全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数约为
全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数约为![]() 人;
人;![]() 这个说法不正确,理由见解析.
这个说法不正确,理由见解析.
【解析】分析:(1)用“经常参加”所占的百分比乘以360°计算即可得解;
(2)先求出“经常参加”的人数,然后求出喜欢篮球的人数,再补全统计图即可;
(3)用总人数乘以喜欢篮球的学生所占的百分比计算即可得解;
(4)根据喜欢乒乓球的27人都是“经常参加”的学生,“偶尔参加”的学生中也会有喜欢乒乓球的考虑解答.
详解:(1)360°×(1﹣15%﹣45%)=360°×40%=144°;
故答案为:144°;
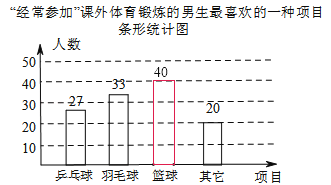
(2)“经常参加”的人数为:300×40%=120人,喜欢篮球的学生人数为:120﹣27﹣33﹣20=120﹣80=40人;
补全统计图如图所示;
(3)全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数约为:1200×![]() =160人;
=160人;
(4)这个说法不正确.
理由如下:小明得到的108人是全校经常参加课外体育锻炼的男生中最喜欢的项目是乒乓球的人数,而全校偶尔参加课外体育锻炼的男生中也会有最喜欢乒乓球的,因此应多于108人.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知P(1,2).
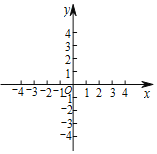
(1)在平面直角坐标系中描出点P(保留画图痕迹);
(2)如果将点P向左平移3个单位长度,再向上平移1个单位长度得到点P',则点P'的坐标为 .
(3)点A在坐标轴上,若S△OAP=2,直接写出满足条件的点A的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,![]() 是函数
是函数![]() 的图像上一点,
的图像上一点,![]() 是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
是y轴上一动点,四边形ABPQ是正方形(点A.B.P.Q按顺时针方向排列)。
(1)求a的值;
(2)如图②,当![]() 时,求点P的坐标;
时,求点P的坐标;
(3)若点P也在函数![]() 的图像上,求b的值;
的图像上,求b的值;
(4)设正方形ABPQ的中心为M,点N是函数![]() 的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
的图像上一点,判断以点P.Q.M.N为顶点的四边形能否是正方形,如果能,请直接写出b的值,如果不能,请说明理由。
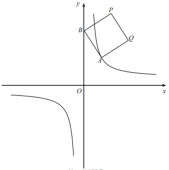
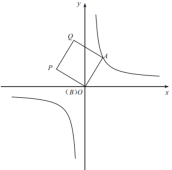

图① 图② 备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情景】利用三角形的面积相等来求解的方法是一种常见的等积法,此方法是我们解决几何问题的途径之一.
例如:张老师给小聪提出这样一个问题:
如图1,在△ABC中,AB=3,AD=6,问△ABC的高AD与CE的比是多少?
小聪的计算思路是:
根据题意得:S△ABC=![]() BCAD=
BCAD=![]() ABCE.
ABCE.
从而得2AD=CE,∴![]()
请运用上述材料中所积累的经验和方法解决下列问题:
(1)【类比探究】
如图2,在ABCD中,点E、F分别在AD,CD上,且AF=CE,并相交于点O,连接BE、BF,
求证:BO平分角AOC.
(2)【探究延伸】
如图3,已知直线m∥n,点A、C是直线m上两点,点B、D是直线n上两点,点P是线段CD中点,且∠APB=90°,两平行线m、n间的距离为4.求证:PAPB=2AB.
(3)【迁移应用】
如图4,E为AB边上一点,ED⊥AD,CE⊥CB,垂足分别为D,C,∠DAB=∠B,AB=![]() ,BC=2,AC=
,BC=2,AC=![]() ,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
,又已知M、N分别为AE、BE的中点,连接DM、CN.求△DEM与△CEN的周长之和.
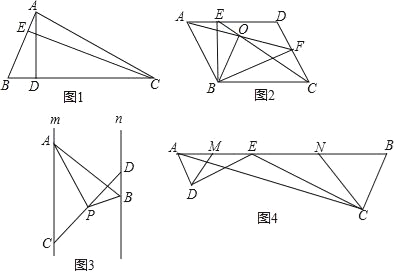
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一个正方形ABCD,点P是边BC上一点.将![]() 绕点A逆时针方向旋转90°得到
绕点A逆时针方向旋转90°得到![]() (点B,P的对应点分别是
(点B,P的对应点分别是![]() )
)
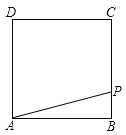
(1)画出旋转后所得到的![]() ;
;
(2)联结![]() ,设
,设![]() ,
,![]() ,试用
,试用![]() 表示
表示![]() 的面积;
的面积;
(3)若![]() 的面积为18,
的面积为18,![]() 的面积为5,试求PC的长.
的面积为5,试求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的顶点叠放在一起.
(1)若∠DCE=25°,求∠ACB的度数.
(2)若∠ACB=140°,求∠DCE的度数.
(3)猜想∠ACB与∠DCE的关系,并说明理由.
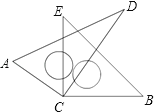
查看答案和解析>>
科目:初中数学 来源: 题型:
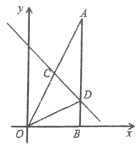
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,直线y=-x+b分别交OA、AB于点C、D,且ΔBOD的面积是4.
(1)求直线AO的解析式;
(2)求直线CD的解析式;
(3)若点M是x轴上的点,且使得点M到点A和点C的距离之和最小,求点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com