
����Ŀ����Rt��ABC��,��ACB= 90��,AC= 6cm, AB= 12cm,��P ��A������AC��C����1cm/s���ٶ������ƶ�;��Q��C������CB��B����![]() cm/s���ٶ������ƶ�����P��Q�ֱ�����ͬʱ�������ƶ���ijһλ��ʱ����ʱ��Ϊt��;��0ΪAB���е㡣
cm/s���ٶ������ƶ�����P��Q�ֱ�����ͬʱ�������ƶ���ijһλ��ʱ����ʱ��Ϊt��;��0ΪAB���е㡣
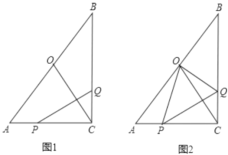
(1)��t=2ʱ�����߶�PQ�ij���;
(2) ����OC,��PQ��0Cʱ�����t��ֵ;
(3)����PO��PQ,�Ƿ����t��ֵ��ʹ��OPQ��Ϊ��PQΪб�ߵ�ֱ��������?�����ڣ����t��ֵ;�������ڣ���˵�����ɡ�
���𰸡���1��![]() ��
��
��2��![]() ��
��
��3�����ڣ�![]() .
.
��������
��1�����˶�ʱ����2�룬���PC��CQ���ù��ɶ�����⼴�ɣ�
��2����ֱ�������ε����ʣ��жϳ���ACO=60�������PQ��OC�ó���CPQ=30�����������Ǻ�����⼴�ɣ�
��3������ֱ�������ε����ʺ���λ�ߣ��ó���PON=��MOQ�����õȽǵ�����ֵ��Ƚ������̣�������������ۼ��㼴�ɣ�
�⣺�ߵ�P��A������AC��C����1cm/s���ٶ������ƶ���
��AP=t��
��CP=6-t��
�ߵ�Q��C������CB��B����![]() cm/s���ٶ������ƶ���
cm/s���ٶ������ƶ���
��![]() ��
��
��1����t=2ʱ��PC=4��CQ=![]() ��
��
�ߡ�ACB=90����
���ݹ��ɶ����ã�![]() ��
��
��2����Rt��ABC����ACB=90����AC=6cm��AB=12cm��
���B=30������A=60����BC=![]()
![]() ��
��
�ߵ�OΪAB�е㣬
��OA=OC��
���ACO=60����
��OC��PQ�Ľ���ΪD��
��PQ��OC��
���PDC=90����
���CPQ=30����
��Rt��PCQ��![]() ��
��
��![]() ��
��
��3�����ڣ���ͼ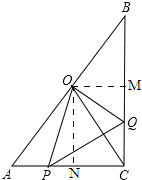
����O��ON��AC��OM��BC��
�ߵ�O��AB�е㣬
��![]()
![]()
![]() ��
��![]() ��
��![]() ��
��
�ߡ�OPQ��Ϊ��PQΪб�ߵ�ֱ�������Σ�
���PON=��MOQ��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]()
�� ��![]() ʱ��
ʱ��![]() ��
��![]() ��
��
��![]()
��![]() ��
��
�� ��![]() ʱ��
ʱ��
![]() ��
��![]() ��
��
��![]() ��
��
��![]() ���ᣩ��������������ڣ�
���ᣩ��������������ڣ�
�������ڣ�![]() ʱ����OPQ��Ϊ��PQΪб�ߵ�ֱ�������Σ�
ʱ����OPQ��Ϊ��PQΪб�ߵ�ֱ�������Σ�


 ����С״Ԫ��������������ϵ�д�
����С״Ԫ��������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ��̣�x-3��(x-2)-p2=0.
��1����֤������pȡ��ֵʱ������������������ȵ�ʵ������
��2���跽����ʵ�����ֱ�Ϊx1��x2��������x12+x22=3 x1x2����ʵ��p��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
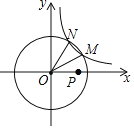
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y=![]() ��k��0����ͼ����뾶Ϊ5�ġ�O����M��N���㣬��MON�����Ϊ3.5��������P��x���ϣ���PM+PN����Сֵ��_____��
��k��0����ͼ����뾶Ϊ5�ġ�O����M��N���㣬��MON�����Ϊ3.5��������P��x���ϣ���PM+PN����Сֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
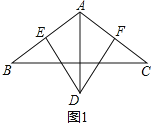
����Ŀ������ABC�У�AB=AC����BAC=120��AD��BC����AD=AB��
��1����ͼ1��DE��AB��DF��AC������ֱ�Ϊ��E��F����֤��AE+AF=AD
��2����ͼ2�������EDF=60������EDF���߷ֱ�AB��AC�ڵ�E��F����ô�߶�AE��AF��AD֮����������������ϵ��������֤����
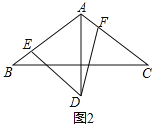
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺����һ����x�����ǰ�[x]����x�����������x��0����[x]��x��1����x��0����[x]��x+1������[0.5]����0.5��
��1����[![]() ]��[��1]��ֵ��
]��[��1]��ֵ��
��2����a��0��b��0ʱ����[a]��[b]���������ʽ��b��a��3��3a+3b��ֵ��
��3���ⷽ�̣�[x]+[x+2]��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���![]() ��
��![]() Ϊ���㣬A��2����3����B��4����3������ֱ��
Ϊ���㣬A��2����3����B��4����3������ֱ��![]() ��
��![]() ��
��![]() ��һ���㣬
��һ���㣬![]() ��AB�ľ���Ϊ6��
��AB�ľ���Ϊ6��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬�����и�ֵ�����߶�
���е㣬�����и�ֵ�����߶�![]() �ij���ʼ��Ϊ1����
�ij���ʼ��Ϊ1����![]() ���ܳ��̶����䣻��
���ܳ��̶����䣻��![]() ������̶����䣻�������ڵ�Qʹ���ı���APBQ��ƽ���ı��Σ���Q��
������̶����䣻�������ڵ�Qʹ���ı���APBQ��ƽ���ı��Σ���Q��![]() ���ڵ�ֱ�ߵľ����Ϊ9������˵����ȷ����__������ţ�
���ڵ�ֱ�ߵľ����Ϊ9������˵����ȷ����__������ţ�
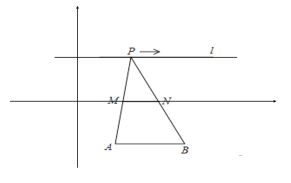
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ӣ����ѧΪ�˽��п�������Ŀѵ�������ȫУ���꼶ѧ���������ȡ�˲���ѧ������һ���п�������Ŀ����(�Ѳ��Խ����Ϊ�ĸ��ȼ���A�������㣻B�������ã�C�����ϸ�D�������ϸ�)���������Խ�����������������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺
��1���γ������Ե�ѧ�����������������ˣ�
��2��ͼ2������ͳ��ͼC�������������������ˣ�
��3����У���꼶��ѧ��500�������ȫ���μ�����п�������Ŀ���ԣ�����Ʋ����������Լ�ж����ˣ�
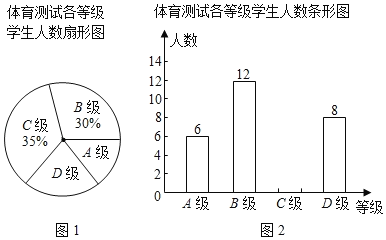
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
��1��![]() = �� ��2��
= �� ��2��![]() = �� ��3��
= �� ��3��![]() ��
��
��4��![]() �� ��5��
�� ��5��![]() �� ��6��a3��a3�� ��
�� ��6��a3��a3�� ��
��7�� (x3)5�� �� ��8��(��2x2y3)3�� �� ��9�� (x��y)6��(x��y)3�� ��
��10��a2b(ab-4b2) ��11����2a-3b����2a+5b��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD��������A��AE��DC������ΪE������BE��FΪBE��һ�����ҡ�AFE����D.
(1)��֤����ABF�ס�BEC��
(2)��AD��5��AB��8��AE��AD��4��5����AF�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com