
【题目】如图,在ABCD中,过点A作AE⊥DC,垂足为E,连接BE,F为BE上一点,且∠AFE=∠D.
(1)求证:△ABF∽△BEC;
(2)若AD=5,AB=8,AE∶AD=4∶5,求AF的长.

【答案】(1)见解析;(2)2![]() .
.
【解析】(1)由平行四边形的性质得出AB∥CD,AD∥BC,AD=BC,得出∠D+∠C=180°,∠ABF=∠BEC,证出∠C=∠AFB,即可得出结论;
(2)由勾股定理求出BE,由AE∶AD=4∶5,求出AE,再由相似三角形的性质求出AF的长.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,
∴∠D+∠C=180°,∠ABF=∠BEC.
∵∠AFB+∠AFE=180°,∠AFE=∠D,
∴∠C=∠AFB,
∴△ABF∽△BEC.
(2)∵AE⊥DC,AB∥DC,
∴∠AED=∠BAE=90°.
∵AD=5, AE∶AD=4∶5,
∴AE=AD×![]() =5×
=5×![]() =4,
=4,
在Rt△ABE中,根据勾股定理,得
BE=![]() =
=![]() =4
=4![]() .
.
在ABCD中,BC=AD=5.
由(1)得△ABF∽△BEC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴AF=2![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB= 90°,AC= 6cm, AB= 12cm,点P 从A出发沿AC向C点以1cm/s的速度匀速移动;点Q从C出发沿CB向B点以![]() cm/s的速度匀速移动,点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒;点0为AB的中点。
cm/s的速度匀速移动,点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒;点0为AB的中点。
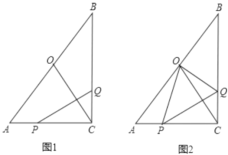
(1)当t=2时,求线段PQ的长度;
(2) 连接OC,当PQ⊥0C时,求出t的值;
(3)连结PO,PQ,是否存在t的值,使△OPQ成为以PQ为斜边的直角三角形?若存在,求出t的值;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,3×3的方格分为上中下三层,第一层有一枚黑色方块甲,可在方格A、B、C中移动,第二层有两枚固定不动的黑色方块,第三层有一枚黑色方块乙,可在方格D、E、F中移动,甲、乙移入方格后,四枚黑色方块构成各种拼图.
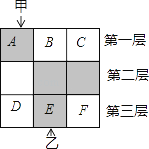
(1)若乙固定在E处,移动甲后黑色方块构成的拼图是轴对称图形的概率是________.
(2)若甲、乙均可在本层移动.
①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率.
②黑色方块所构拼图是中心对称图形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:公路旁有两个高度相等的路灯AB、CD.数学老师杨柳上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
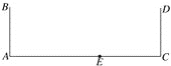
(1)在图中画出杨老师的位置(用线段FG表示),并画出光线,标明(太阳光、灯光);
(2)若上午上学时候高1米的木棒的影子为2米,杨老师身高为1.5米,他离里程碑E恰5米,求路灯高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
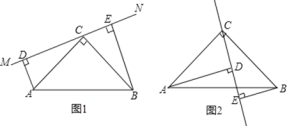
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016江苏省连云港市)环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
(1)求整改过程中硫化物的浓度y与时间x的函数表达式;
(2)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将7张相同的小长方形纸片(如图1所示)按图2所示的方式不重叠的放在长方形ABCD内,未被覆盖的部分恰好被分割为两个长方形,面积分别为S1,S2,已知小长方形纸片的长为a,宽为b,且a>b
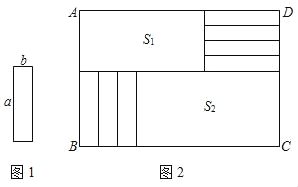
(1)当a=9,b=2,AD=30时,请求:
①长方形ABCD的面积;
②S2﹣S1的值.
(2)当AD=30时,请用含a,b的式子表示S2﹣S1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com