Question

【题目】如图1在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．

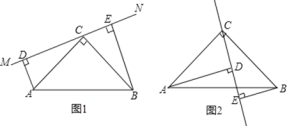
（1）求证：①△ADC≌△CEB；②DE=AD+BE．

（2）当直线MN绕点C旋转到图2的位置时，DE、AD、BE又怎样的关系？并加以证明．

Answer 1

【答案】（1）①见解析，②见解析；（2）DE=AD－BE，证明见解析.

【解析】

（1）①先利用同角的余角相等证得∠DAC=∠ECB，再根据AAS即可证得结论；②根据①的结论可得AD=CE，DC=EB，进一步即得结论；

（2）同（1）的证法得出△ADC≌△CEB，根据全等三角形的性质可得AD=CE，DC=BE，进一步即可得出结论.

（1）证明：①∵∠ACD+∠ACB+∠BCE=180°，∠ACB=90°，

∴∠ACD+∠BCE=90°．

∵AD⊥MN，BE⊥MN，

∴∠ADC=∠CEB=90°，∠DAC+∠ACD=90°，

∴∠DAC=∠ECB，

在△ADC和△CEB中，

∴△ADC≌△CEB（AAS）.

②由①知：△ADC≌△CEB，

∴AD=CE，DC=EB，

∵DE=CE+DC，

∴DE=AD+EB；

（2）DE=AD－BE.

证明：∵AD⊥CE，BE⊥CE，

∴∠ADC=∠BEC=90°，∠EBC+∠ECB=90°，

∵∠ACB=90°，

∴∠ECB+∠ACE=90°，

∴∠ACD=∠EBC.

在△ADC和△CEB中，

∴△ADC≌△CEB（AAS），

∴AD=CE，DC=BE，

∴DE=CE－CD=AD－BE．