
【题目】操作发现:
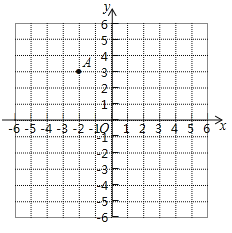
(1)如图,在平面直角坐标系中有一点![]() ,将点
,将点![]() 先向右平移3个单位长度,再向下平移3个单位长度得到点
先向右平移3个单位长度,再向下平移3个单位长度得到点![]() ,则点
,则点![]() 的坐标为 ;并在图中画出直线
的坐标为 ;并在图中画出直线![]() 的函数图象;
的函数图象;
(2)直接写出直线![]() 的解析式 ;
的解析式 ;
(3)若直线![]() 上有一动点
上有一动点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
①直接写出点![]() 的坐标 ;
的坐标 ;
②若点![]() 位于第四象限,直接写出三角形
位于第四象限,直接写出三角形![]() 的面积 .(用含
的面积 .(用含![]() 的式子表示)
的式子表示)
【答案】(1)B(1,0),画图见解析;(2)![]() ;(3)①
;(3)①![]() ;②
;②![]() .
.
【解析】
(1)根据平移的方向和距离可得到点B的坐标,然后连接AB即可;
(2)利用待定系数法求解即可;
(3)①根据一次函数图象上点的坐标特征求解即可;
②求出P到x轴的距离,根据三角形面积公式求解即可.
解:(1)将点A(2,3)先向右平移3个单位长度,再向下平移3个单位长度得到点B,则点B的坐标为(1,0),
画出直线AB如图:

(2)设直线AB的解析式为y=kx+b(k≠0),
代入A(2,3),B(1,0)得![]() ,
,
解得:k=1,b=1,
∴直线AB的解析式为y=x+1;
(3)①∵点P是直线AB上的动点,点P的横坐标为t,
∴y=t+1,
∴P(t,t+1);
②∵点P位于第四象限,
∴P到x轴的距离为t1,
∵OB=1,
∴三角形BOP的面积为:![]() ×1×(t1)=
×1×(t1)=![]() .
.


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
把代数式通过配凑等手段得到局部完全平方式,再进行有关计算和解题,这种解题方法叫做配方法.
如(1)用配方法分解因式:![]() .
.
解:原式=![]()
=![]()
(2)M=![]() ,利用配方法求M的最小值.
,利用配方法求M的最小值.
解:M=![]()
=![]()
![]()
![]() M有最小值1.
M有最小值1.
请根据上述材料,解决下列问题:
(1)在横线上添加一个常数,使之成为完全平方式:![]()
(2)用配方法分解因式:![]()
(3)若M=![]() ,求M的最小值.
,求M的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
(1)求证:△ADB≌△CDE;
(2)求∠MDN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 打开电视机,正在播广告,是必然事件
B. 在连续5次的数学测试中,两名同学的平均分相同,方差较大的同学数学成绩更稳定
C. 某同学连续10次抛掷质量均匀的硬币,3次正面向上,因此正面向上的概率是30%
D. 从一个只装有白球的缸里摸出一个球,摸出的球是白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形平移与旋转”为主题开展数学活动,![]() 和
和![]() 是两个等边三角形纸片,其中,
是两个等边三角形纸片,其中,![]() .
.
解决问题
(1)勤奋小组将![]() 和
和![]() 按图1所示的方式摆放(点
按图1所示的方式摆放(点![]() 在同一条直线上) ,连接
在同一条直线上) ,连接![]() .发现
.发现![]() ,请你给予证明;
,请你给予证明;

(2)如图2,创新小组在勤奋小组的基础上继续探究,将![]() 绕着点
绕着点![]() 逆时针方向旋转,当点
逆时针方向旋转,当点![]() 恰好落在
恰好落在![]() 边上时,求
边上时,求![]() 的面积;
的面积;

拓展延伸
(3)如图3,缜密小组在创新小组的基础上,提出一个问题: “将![]() 沿
沿![]() 方向平移
方向平移![]() 得到
得到![]() 连接
连接![]() ,当
,当![]() 恰好是以
恰好是以![]() 为斜边的直角三角形时,求
为斜边的直角三角形时,求![]() 的值.请你直接写出
的值.请你直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),B(b,0),C(﹣1,2),且|2a﹣b+8|+(a+b﹣2)2=0.

(1)求a、b的值;
(2)如图1,点G在y轴上,三角形COG的面积是三角形ABC的面积的![]() ,求出点G的坐标;
,求出点G的坐标;
(3)如图2,过点C作CD⊥y轴交y轴于点D,点P为线段CD延长线上的一个动点,连接OP、AC、DB,OE平分∠AOP,OF⊥CE,若∠OPD+k∠DOF=k(∠FOP+∠AOE),现将四边形ABDC向下平移![]() k个单位得到四边形A1B1D1C1,已知AM+BN =
k个单位得到四边形A1B1D1C1,已知AM+BN =![]() k,求图中阴影部分的面积.
k,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1:y1=2x+2与直线 l2:y2=mx+8相交于点 P(2,b).
(1)求 b,m 的值;
(2)直接写出当 y1<y2 时,自变量 x 的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点O为直线AB上一点,∠COD=90°,射线OE平分∠AOD.
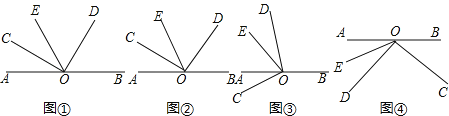
(1)如图①所示,若∠COE=20°,则∠BOD= °.
(2)若将∠COD绕点O旋转至图②的位置,试判断∠BOD和∠COE的数量关系,并说明理由;
(3)若将∠COD绕点O旋转至图③的位置,∠BOD和∠COE的数量关系是否发生变化?并请说明理由.
(4)若将∠COD绕点O旋转至图④的位置,继续探究∠BOD和∠COE的数量关系,请直接写出∠BOD和∠COE之间的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四块完全相同的小长方形拼成的一个“回形”正方形.

(1)用不同代数式表示图中的阴影部分的面积,你能得到怎样的等式:________;
(2)利用(1)中的结论.计算:![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)根据(1)的结论.若![]() .求
.求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com