练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．如图，从边长为a+2的正方形纸片中剪去一个边长为a-2的正方形（a＞2），剩余部分沿线剪开，再拼成一个矩形（不重叠无缝隙），则该矩形的面积是（　　）
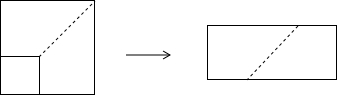
    A．8aB．4aC．2aD．a2-4

    分析 利用大正方形的面积减去小正方形的面积即可，注意完全平方公式的计算．

    解答 解：（a+2）2-（a-2）2
    =（a2+4a+4）-（a2-4a+4）
    =a2+4a+4-a2+4a-4
    =8a．
    故选A．

    点评 本题考查了平方差公式的几何背景，理解大正方形与小正方形的面积的差就是矩形的面积是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．若（　　）×（-3）=1，则括号内填一个实数应该是（　　）
    A．$\frac{1}{3}$B．3C．-3D．-$\frac{1}{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

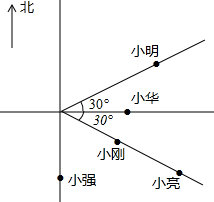    7．小李、小明、小刚、小强、小华、小亮是很要好的伙伴，他们家的位置如图所示．一天，小李说：“如果以我家为中心，你们各自家的位置在哪儿知道吗？”其余小伙伴说到：“当然知道了．”小李说：“这样吧，你们若回答出下列问题，就证明你们知道．”
    （1）南偏东60°的方向上有谁的家？怎样确定小刚家的位置？请你表示出来．
    （2）小明家在什么位置？
    （3）距小李家图上距离为0.9cm处的地方有谁的家？
    （4）想确定他们每个小伙伴的家的位置，各需要哪些数据？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，AB是⊙O的直径，AC是⊙O的切线，连接OC交⊙O于点D，连接BD，∠C=40°．则∠ABD的度数是25°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

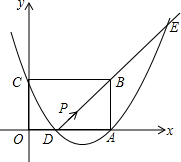    2．如图，已知矩形OABC，点A，C分别在x，y轴上，抛物线y=ax2+bx+c经过A（12，0），D（6，0）两点，且与y轴交于点C（0，8）．动点P从点D出发，以每秒1个单位的速度沿射线DB方向运动，设P运动的时间为t（秒），射线DB交抛物线于E．
    （1）求抛物线的解析式；
    （2）连结AP，是否存在这样的时刻t，使得∠PAB=∠ADB？若存在请求出t的值；若不存在，请说明理由．
    （3）连结CP和AE，若∠PCB＜∠AED，求t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

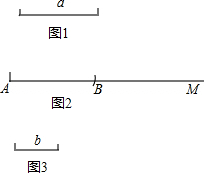    12．阅读材料：用尺规作图要求作线段AB等于线段a时，小明的具体作法如下：
    已知：线段a，如图1
    求作：线段AB，使得线段AB=a．
    解：作图步骤如下“
    ①作射线AM；
    ②用圆规在射线AM上截取AB=a，如图2．
    ∴线段AB为所求作的线段．
    解决下列问题：
    已知：线段b，如图3
    （1）请你依照小明的作法，在上图②中的射线AB作线段BD，使BD=b；（不要求写作法和结论，保留作图痕迹，用签字笔加粗）
    （2）在（1）的条件下，取AD的中点E，若AB=3，BD=2，求线段BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，为了把△ABC平移得到△A′B′C′，可以先将∠ABC向右平移5格，再向上平移3格．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．设m和n均不为零，3x2y3和-5x2+2m+ny3是同类项，则$\frac{3{m}^{3}-{m}^{2}n+3m{n}^{2}+9{n}^{3}}{5{m}^{2}+3{m}^{2}n-6m{n}^{2}+9{n}^{3}}$=$\frac{55}{97}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．下列四个命题中，它的逆命题成立的是（　　）
    A．如果x=y，那么x2=y2B．直角都相等
    C．全等三角形对应角相等D．等边三角形的每个角都等于60°

    查看答案和解析>>

    同步练习册答案