
【题目】如图1,抛物线y=﹣x2+bx+c与x轴交于A(2,0),B(﹣4,0)两点.

(1)求该抛物线的解析式;
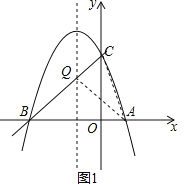
(2)若抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
(3)在抛物线的第二象限图象上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC的面积最大值;若不存,请说明理由.
【答案】(1):y=﹣x2﹣2x+8;(2)点Q(﹣1,6)即为所求;(3)点P的坐标为(﹣2,8).
【解析】
试题分析:(1)直接利用待定系数求出二次函数解析式即可;
(2)首先求出直线BC的解析式,再利用轴对称求最短路线的方法得出答案;
(3)根据S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣16,得出函数最值,进而求出P点坐标即可.
解:(1)将A(2,0),B(﹣4,0)代入得:
![]() ,
,
解得:![]() ,
,
则该抛物线的解析式为:y=﹣x2﹣2x+8;
(2)如图1,点A关于抛物线对称轴的对称点为点B,设直线BC的解析式为:y=kx+d,
将点B(﹣4,0)、C(0,8)代入得:
![]() ,
,
解得:![]() ,
,
故直线BC解析式为:y=2x+8,
直线BC与抛物线对称轴 x=﹣1的交点为Q,此时△QAC的周长最小.
解方程组![]() 得,
得,![]()
则点Q(﹣1,6)即为所求;
(3)如图2,过点P作PE⊥x轴于点E,
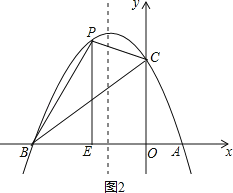
P点(x,﹣x2﹣2x+8)(﹣4<x<0)
∵S△BPC=S四边形BPCO﹣S△BOC=S四边形BPCO﹣16
若S四边形BPCO有最大值,则S△BPC就最大
∴S四边形BPCO=S△BPE+S直角梯形PEOC
=![]() BEPE+
BEPE+![]() OE(PE+OC)
OE(PE+OC)
=![]() (x+4)(﹣x2﹣2x+8)+
(x+4)(﹣x2﹣2x+8)+![]() (﹣x)(﹣x2﹣2x+8+8)
(﹣x)(﹣x2﹣2x+8+8)
=﹣2(x+2)2+24,
当x=﹣2时,S四边形BPCO最大值=24,
∴S△BPC最大=24﹣16=8,
当x=﹣2时,﹣x2﹣2x+8=8,
∴点P的坐标为(﹣2,8).


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠ABC=90°,利用直尺和圆规,根据要求作图(不写作法,保留作图痕迹),并解决下面的问题.
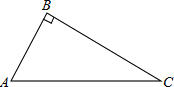
(1)作AC的垂直平分线,分别交AC、BC于点D、E;
(2)若AB=12,BE=5,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
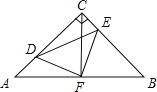
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某报亭老板以每份0.5元的价格从报社购进某种报纸500份,以每份0.8元的价格销售x份﹙x<500﹚,未销售完的报纸又以每份0.1元的价格由报社收回。这次买卖中该老板赚钱____元。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是∠ABC平分线,DE⊥AB于E,AB=36cm,BC=24cm,S△ABC=144cm2,则DE的长是( )
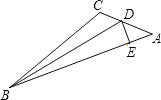
A.4.8cm B.4.5cm C.4cm D.2.4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
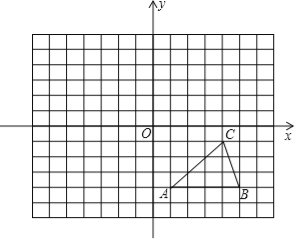
(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
(2)以原点O为对称中心,再画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com