
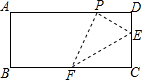
 如图,在矩形ABCD中,点E、F分别在边CD和BC上,且CD=4DE=4a,将矩形沿直线EF折叠,使点C恰好落在AD边上点P处,则FP=3$\sqrt{2}$a.
如图,在矩形ABCD中,点E、F分别在边CD和BC上,且CD=4DE=4a,将矩形沿直线EF折叠,使点C恰好落在AD边上点P处,则FP=3$\sqrt{2}$a. 分析 作PM⊥BC于M,则MP=DC=4a,由矩形的性质得出∠C=∠D=90°.由折叠的性质得出PE=CE=3a=3DE,∠EPF=∠C=90°,得出∠DPE=∠FPM,在Rt△MPF中,由三角函数求出FP即可.
解答 解:作PM⊥BC于M,如图所示: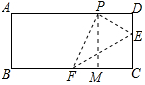
则MP=DC=4a,
∵四边形ABCD是矩形,
∴∠C=∠D=∠MPD=90°.
∵DC=4DE=4a,
∴CE=3a,DE=a,
由折叠的性质得:PE=CE=3a=3DE,∠EPF=∠C=90°,
∴∠EPF=∠MPD
∴∠DPE=∠FPM,
DP=$\sqrt{P{E}^{2}-D{E}^{2}}$=$\sqrt{(3a)^{2}-{a}^{2}}$=2$\sqrt{2}$a,
在Rt△MPF中,∵cos∠MPF=$\frac{PM}{PF}$,
∴FP=$\frac{PM}{cos∠MPF}$=$\frac{PM}{cos∠DPE}$=$\frac{PM}{\frac{PD}{PE}}$=$\frac{4a}{\frac{2\sqrt{2}a}{3a}}$=3$\sqrt{2}$a;
故答案为:3$\sqrt{2}$a.
点评 本题考查了折叠的性质、矩形的性质、三角函数等知识;熟练掌握折叠和矩形的性质,求出∠DPE的余弦值是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 已知,如图,⊙O是△ABC的外接圆,OD⊥BC交⊙O于点D,CE平分∠ACB交AB于点E,交⊙O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.
已知,如图,⊙O是△ABC的外接圆,OD⊥BC交⊙O于点D,CE平分∠ACB交AB于点E,交⊙O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )
如图1,A、B、C三点在正方形网格线的交点处,若将△ACB逆时针旋转得到△AC′B′,则tanB′的值为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,Rt△ABC的顶点B在原点O,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3,$\sqrt{3}$),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是(2,0)或(4,0).
如图,在平面直角坐标系中,Rt△ABC的顶点B在原点O,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3,$\sqrt{3}$),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是(2,0)或(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
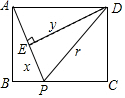 如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )| A. | 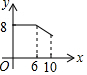 | B. | 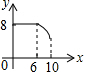 | C. |  | D. | 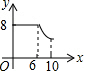 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{2}+{b}^{2}}{a+b}$ | B. | $\frac{{x}^{2}+2x+1}{x+1}$ | C. | $\frac{2ax}{3ay}$ | D. | $\frac{{a}^{2}-{b}^{2}}{a-b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
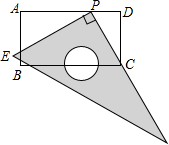 如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E.
如图,在矩形ABCD中,AB=6,AD=11.直角尺的直角顶点P在AD上滑动时(点P与A,D不重合),一直角边始终经过点C,另一直角边与AB交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
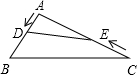 如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )
如图,在钝角△ABC中,AB=5cm,AC=10cm,动点D从A点出发到B点止,动点E从C点出发到A点止,点D运动的速度为1cm/秒,点E运动的速度为2cm/秒,如果两点同时运动,那么当以点A、D、E为顶点的三角形与△ABC相似时,运动的时间是( )| A. | 2.5秒 | B. | 4.5秒 | C. | 2.5秒或4.5秒 | D. | 2.5秒或4秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com