
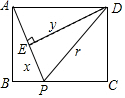
 如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
如图,矩形ABCD中,AB=6,BC=8,动点P从点A出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )| A. | 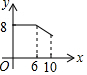 | B. | 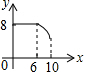 | C. |  | D. | 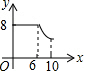 |
分析 ①点P在AB上时,点D到AP的距离为AD的长度,②点P在BC上时,根据同角的余角相等求出∠APB=∠PAD,再利用相似三角形的性质列出比例式整理得到y与x的关系式,从而得解.
解答  解:①点P在AB上时,0≤x≤6,点D到AP的距离为AD的长度,是定值8;
解:①点P在AB上时,0≤x≤6,点D到AP的距离为AD的长度,是定值8;
②点P在BC上时,6<x≤10,
∵∠APB+∠BAP=90°,
∠PAD+∠BAP=90°,
∴∠APB=∠PAD,
又∵∠B=∠DEA=90°,
∴△ABP∽△DEA,
∴$\frac{AB}{DE}$=$\frac{AP}{AD}$,
即$\frac{6}{y}$=$\frac{x}{8}$,
∴y=$\frac{24}{x}$,
纵观各选项,只有D选项图形符合.
故选:D.
点评 本题考查了动点问题函数图象,关键是利用了相似三角形的判定与性质,难点在于根据点P的位置分两种情况讨论.


科目:初中数学 来源: 题型:填空题
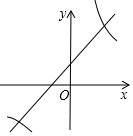 反比例函数y=$\frac{6}{x}$与一次函数y=x+1的图象交于点A(2,3),利用图象的对称性可知它们的另一个交点是(-3,2),$\frac{6}{x}$<x+1的解集为-3<x<0或x>2.
反比例函数y=$\frac{6}{x}$与一次函数y=x+1的图象交于点A(2,3),利用图象的对称性可知它们的另一个交点是(-3,2),$\frac{6}{x}$<x+1的解集为-3<x<0或x>2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
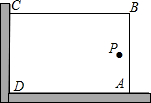 我县一小区为了美化环境,打算借助如图所示的直角墙角(两边足够长),用28m长的围栏围成一个矩形花园ABCD(围栏只围AB、BC两边)
我县一小区为了美化环境,打算借助如图所示的直角墙角(两边足够长),用28m长的围栏围成一个矩形花园ABCD(围栏只围AB、BC两边)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | $\frac{5}{2}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
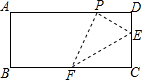 如图,在矩形ABCD中,点E、F分别在边CD和BC上,且CD=4DE=4a,将矩形沿直线EF折叠,使点C恰好落在AD边上点P处,则FP=3$\sqrt{2}$a.
如图,在矩形ABCD中,点E、F分别在边CD和BC上,且CD=4DE=4a,将矩形沿直线EF折叠,使点C恰好落在AD边上点P处,则FP=3$\sqrt{2}$a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
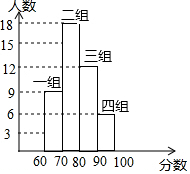 某校七(3)班的同学进行了一次安全知识测试,测试成绩进行整理后分成四个组,并绘制如图所示的频数直方图,则第二组的频数是( )
某校七(3)班的同学进行了一次安全知识测试,测试成绩进行整理后分成四个组,并绘制如图所示的频数直方图,则第二组的频数是( )| A. | 0.4 | B. | 18 | C. | 0.6 | D. | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
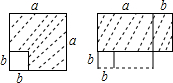 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com