
 已知,如图,⊙O是△ABC的外接圆,OD⊥BC交⊙O于点D,CE平分∠ACB交AB于点E,交⊙O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF.
已知,如图,⊙O是△ABC的外接圆,OD⊥BC交⊙O于点D,CE平分∠ACB交AB于点E,交⊙O于点H,AD与CH相交于点G,延长CH到点M,使MH=HG,延长DA到点K,使AK=AG,CA的延长线交MK于点F,求证:ME=MF. 分析 如图,连接AH、AM.首先证明∠HGA=∠HAG,推出HA=GH=HM,推出△MAG是直角三角形,即MA⊥KG,因为AG=AK,所以MG=MK,再证明△AGE≌△AKF,得EG=FK,即可解决问题.
解答 证明:如图,连接AH、AM.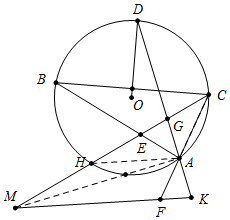
∵OD⊥BC,
∴$\widehat{DB}$=$\widehat{DC}$,
∴∠BAD=∠CAD,
∵∠BCH=∠ACH,∠BCH=∠BAH,
∴∠BAH=∠ACH,
∵∠HGA=∠ACH+∠CAG,∠HAG=∠BAH+∠BAD,
∴∠HGA=∠HAG,
∴HA=GH=HM,
∴△MAG是直角三角形,
∴MA⊥KG,
∵AG=AK,
∴MG=MK,
∴∠AGE=∠K,
∵∠FAK=∠CAD,∠BAD=∠DAC,
∴∠EAG=∠FAK,
在△AGE和△AKF中,
$\left\{\begin{array}{l}{∠AGE=∠K}\\{AG=AK}\\{∠EAG=∠FAK}\end{array}\right.$,
∴△AGE≌△AKF,
∴EG=FK,∵MG=MK,
∴ME=MF.
点评 本题考查圆综合题、直角三角形的判定、全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,本题的突破点是证明AM⊥GK,学会添加常用辅助线,所以中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 某企业生产并销售某种产品,假设销售量与产量相等,图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
某企业生产并销售某种产品,假设销售量与产量相等,图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
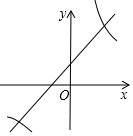 反比例函数y=$\frac{6}{x}$与一次函数y=x+1的图象交于点A(2,3),利用图象的对称性可知它们的另一个交点是(-3,2),$\frac{6}{x}$<x+1的解集为-3<x<0或x>2.
反比例函数y=$\frac{6}{x}$与一次函数y=x+1的图象交于点A(2,3),利用图象的对称性可知它们的另一个交点是(-3,2),$\frac{6}{x}$<x+1的解集为-3<x<0或x>2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为点D、E.
如图所示,已知△ABC中,∠BAC=90°,AB=AC,MN是经过点A的直线,BD⊥MN,CE⊥MN,垂足分别为点D、E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
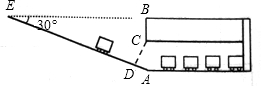 某校九年级数学兴趣小组为了测得该校地下停车场的限高CD(CD⊥AE),在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米,试求该校地下停车场的高度AC及限高CD($\sqrt{3}$≈1.73,结果精确到0.1米)
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD(CD⊥AE),在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为30°,斜坡AE的长为16米,地面B点(与E点在同一水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.2米,试求该校地下停车场的高度AC及限高CD($\sqrt{3}$≈1.73,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
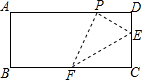 如图,在矩形ABCD中,点E、F分别在边CD和BC上,且CD=4DE=4a,将矩形沿直线EF折叠,使点C恰好落在AD边上点P处,则FP=3$\sqrt{2}$a.
如图,在矩形ABCD中,点E、F分别在边CD和BC上,且CD=4DE=4a,将矩形沿直线EF折叠,使点C恰好落在AD边上点P处,则FP=3$\sqrt{2}$a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com