
 如图所示,四边形ABCD是一个边长为90米的正方形,甲在A处,乙在B处,两人同时出发,都沿A→B→C→D→A…的方向行走,甲每分钟走65米,乙每分钟走72米,则两人第一次相遇在正方形的哪条边上?
如图所示,四边形ABCD是一个边长为90米的正方形,甲在A处,乙在B处,两人同时出发,都沿A→B→C→D→A…的方向行走,甲每分钟走65米,乙每分钟走72米,则两人第一次相遇在正方形的哪条边上? 科目:初中数学 来源: 题型:解答题
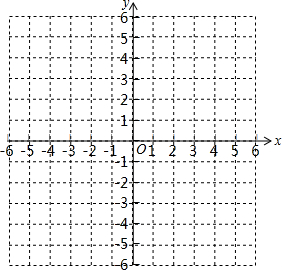 在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:
在如图的直角坐标系中,画出函数y=-2x+3的图象,并结合图象回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
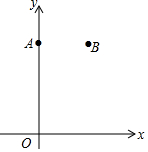 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
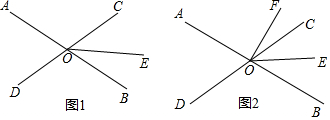
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
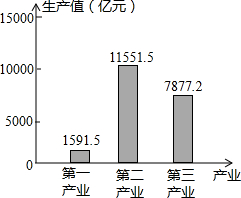 如图是2002年第一季度国内生产总值(亿元)统计图
如图是2002年第一季度国内生产总值(亿元)统计图查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com