练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，CD是⊙O的弦，O是圆心，把⊙O的劣弧沿着CD对折，A是对折后劣弧上的一点，∠CAD=110°，则∠B的度数是（ ）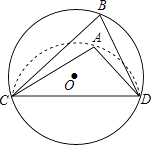

    A.110°
    B.70°
    C.60°
    D.55°

    【答案】B
    【解析】解：如图，翻折△ACD，点A落在A'处，

    ∴∠A'=∠A=110°，

    ∵四边形A'CBD是⊙O的内接四边形，

    ∴∠A'+∠B=180°，

    ∴∠B=70°，

    所以答案是：B．

    【考点精析】认真审题，首先需要了解圆内接四边形的性质(把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线，以相邻切线的交点为顶点的多边形是这个圆的外切正n边形)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】南沙群岛是我国的固有领土，现在我南海渔民要在南沙群岛某海岛附近进行捕鱼作业，当渔船航行至B处时，测得该岛位于正北方向20（1＋ ）海里的C处，为防止某国的巡警干扰，就请求我A处的鱼监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西30°的方向上，求A、C之间的距离．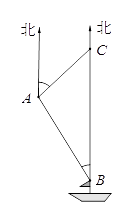

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某工厂新开发生产一种机器，每台机器成本y（万元）与生产数量x（台）之间满足一次函数关系（其中10≤x≤70，且为整数），函数y与自变量x的部分对应值如表

    x单位：台）

    10

    20

    30

    y（单位：万元/台）

    60

    55

    50

    （1）求y与x之间的函数关系式；

    （2）市场调查发现，这种机器每月销售量z（台）与售价a（万元/台）之间满足如图所示的函数关系．

    ①该厂第一个月生产的这种机器40台都按同一售价全部售出，请求出该厂第一个月销售这种机器的总利润．（注：利润＝售价﹣成本）

    ②若该厂每月生产的这种机器当月全部售出，则每个月生产多少台这种机器才能使每台机器的利润最大？

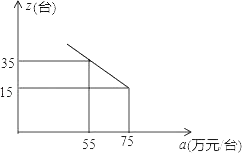
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知y是x的一次函数，当x＝1时，y＝1；当x＝－2时，y＝－14.

    (1)求这个一次函数的关系式；

    (2)在如图所示的平面直角坐标系中作出函数的图像；

    (3)由图像观察，当0≤x≤2时，函数y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在某市开展的“体育、艺术2＋1”活动中，某校根据实际情况，决定主要开设A：乒乓球，B：篮球，C：跑步，D：跳绳这四种运动项目．为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如图甲、乙所示的条形统计图和扇形统计图．请你结合图中的信息解答下列问题：

    (1)求出所抽取的学生人数，并把条形统计图补充完整；

    (2)样本中喜欢B项目的人数百分比是 ，其所在扇形统计图中的圆心角的度数是 ；

    (3)已知该校有1 000人，根据样本估计全校喜欢跳绳的人数是多少？

    图甲 图乙

    查看答案和解析>>

    科目：初中数学 来源： 题型：

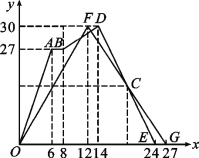
    【题目】甲、乙两组同学玩“两人背夹球”比赛，即：每组两名同学用背部夹着球跑完规定的路程，若途中球掉下时须捡起并回到掉球处继续赛跑，用时少者胜．结果：甲组两位同学掉了球；乙组两位同学顺利跑完．设比赛中同学距出发点的距离用y表示，单位是米；比赛时间用x表示，单位是秒．两组同学比赛过程用图像表示如下：

    (1)这是一次 米的背夹球比赛；

    (2)线段 表示甲组两位同学在比赛中途掉球，耽误了 秒；

    (3)甲组同学到达终点用了 秒，乙组同学到达终点用了 秒，获胜的是 组同学；

    (4)请直接写出C点坐标，并说明点C的实际意义．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    某“综合与实践”小组开展了“长方体纸盒的制作”实践活动，他们利用边长为的正方形纸板制作出两种不同方案的长方体盒子（图1为无盖的长方体纸盒，图2为有盖的长方体纸盒），请你动手操作验证并完成任务.（纸板厚度及接缝处忽略不计）

    动手操作一：

    根据图1方式制作一个无盖的长方体盒子.方法：先在纸板四角剪去四个同样大小边长为的小正方形，再沿虚线折合起来．

    问题解决

    （1）该长方体纸盒的底面边长为_______；（请你用含的代数式表示）

    （2）若，，则长方体纸盒的底面积为_______；

    动手操作二：

    根据图2方式制作一个有盖的长方体纸盒．方法：先在纸板四角剪去两个同样大小边长为的小正方形和两个同样大小的小长方形，再沿虚线折合起来．

    拓展延伸

    （3）该长方体纸盒的体积为______；（请你用含的代数式表示）

    （4）现有两张边长均为的正方形纸板，分别按图1、图2的要求制作无盖和有盖的两个长方体盒子，若，求无盖盒子的体积是有盖盒子体积的多少倍．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中，用如下的三角形解释(a+b)n的展开式中各项的系数，此三角形称为“杨辉三角”，

    即：(a+b)1=a+b

    (a+b)2=a2+2ab+b2

    (a+b)3=a3+3a2b+3ab2+b3

    (a+b)4=a4+4a3b+6a2b2+4ab3+b4

    (a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5

    根据“杨辉三角”计算出(a+b)10的展开式中第三项的系数为(　　)

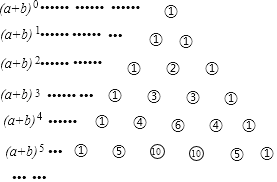
    A.10B.45C.46D.50

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠BAC＝90°，点D是BC上一点，将△ABD沿AD翻折后得到△AED，边AE交BC于点F．

    (1)如图①，当AE⊥BC时，写出图中所有与∠B相等的角：　 ；所有与∠C相等的角：　 　 ．

    (2)若∠C－∠B＝50°，∠BAD＝x°(0＜x≤45) ．

    ① 求∠B的度数；

    ②是否存在这样的x的值，使得△DEF中有两个角相等．若存在，并求x的值；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案