
【题目】规定:二元一次方程![]() 有无数组解,每组解记为
有无数组解,每组解记为![]() ,称
,称![]() 为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
为亮点,将这些亮点连接得到一条直线,称这条直线是亮点的隐线,答下列问题:
(1) 已知![]() ,则是隐线
,则是隐线![]() 的亮点的是 ;
的亮点的是 ;
(2) 设![]() 是隐线
是隐线![]() 的两个亮点,求方程
的两个亮点,求方程![]() 中
中![]() 的最小的正整数解;
的最小的正整数解;
(3)已知![]() 是实数, 且
是实数, 且![]() ,若
,若![]() 是隐线
是隐线![]() 的一个亮点,求隐线
的一个亮点,求隐线![]() 中的最大值和最小值的和.
中的最大值和最小值的和.
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.
与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中, ![]() 的三个顶点都在格点上,点
的三个顶点都在格点上,点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 、
、![]() ,试解答下列问题:
,试解答下列问题:
(1)画出![]() 关于原点
关于原点![]() 对称的
对称的![]() ;
;
(2)平移![]() ,使点
,使点![]() 移到点
移到点![]() ,画出平移后的
,画出平移后的![]() 并写出点
并写出点![]() 、
、![]() 的坐标;
的坐标;
(3)在![]() 、
、![]() 、
、![]() 中,
中, ![]() 与哪个图形成中心对称?试写出其对称中心的坐标.
与哪个图形成中心对称?试写出其对称中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车去韶山研学, 现有甲、乙两种大客车,甲种客车每辆载客量![]() 人,乙种客车每辆载客量
人,乙种客车每辆载客量![]() 人.已知
人.已知![]() 辆甲种客车和
辆甲种客车和![]() 辆乙种客车需租金
辆乙种客车需租金![]() 元,
元,![]() 辆甲种客车和
辆甲种客车和![]() 辆乙种客车共需租金
辆乙种客车共需租金![]() 元.
元.
(1)求![]() 辆甲种客车和
辆甲种客车和![]() 辆乙种客车的租金分别是多少元?
辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共![]() 辆,送
辆,送![]() 名师生集体外出活动,总费用不超过
名师生集体外出活动,总费用不超过![]() 元,则共有哪几种租车方案?
元,则共有哪几种租车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连结OE.下列结论:
BC,连结OE.下列结论:
①∠CAD=30°;②SABCD=AB·AC;③OB=AB;④OE=![]() BC,成立的结论有______.(填序号)
BC,成立的结论有______.(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
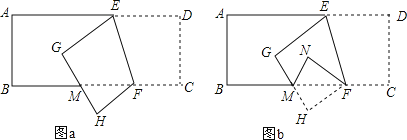
【题目】如图a,已知长方形纸带ABCD,AB∥CD,AD∥BC,∠BFE=70°,将纸带沿EF折叠后,点C、D分别落在H、G的位置,再沿BC折叠成图b.
(1)图a中,∠AEG=______°;
(2)图a中,∠BMG=______°;
(3)图b中,∠EFN=______°.
查看答案和解析>>
科目:初中数学 来源: 题型:
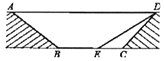
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
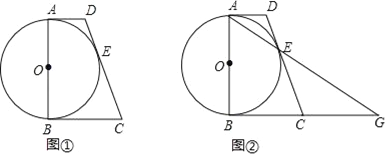
(1)求证:BC为⊙O的切线;
(2)连接AE并延长与BC的延长线交于点G(如图②所示).若AB=![]() ,CD=9,求线段BC和EG的长.
,CD=9,求线段BC和EG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com