Question

【题目】如图①是一张矩形纸片, , .在边上取一点，在边上取一点，将纸片沿折叠，使与交于点，得到，如图②所示.

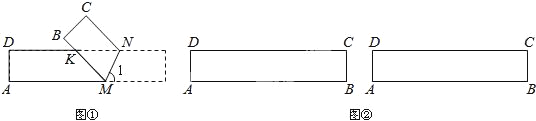
（1）若，求的度数.

（2） 的面积能否小于?若能，求出此时的度数;若不能，试说明理由.

（3）如何折叠能够使的面积最大?请你画图探究可能出现的情况，求出最大值.

Answer 1

【答案】（1） 40°．（2） △MNK的面积不能小于；理由见解析；（3）1.3

【解析】

试题分析：（1）证明∠MKN=∠KMA；证明∠KMN=∠1=70°，即可解决问题．

（2）如图1，作辅助线；证明MK＞1；证明NK=MK＞1，运用三角形的面积公式即可解决问题．

（3）如图2，证明MK=MQ（设为λ），得到AM=5-λ；列出关于λ的方程（5-λ）2+12=λ2，求出λ即可解决问题．

试题解析：（1）如图1，∵四边形ABCD为矩形，

∴DN∥AM，∠MKN=∠KMA；

由题意得：∠KMN=∠1=70°，

∴∠KMA=180°-140°=40°，

∴∠MKN=40°．

（2）△MNK的面积不能小于；理由如下：

如图1，过点M作MP⊥KN；则MP=1；

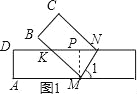
由题意得MK＞1，∠KMN=∠1；

∵KN∥AM，

∴∠KNM=∠1，∠KMN=∠KNM，

∴NK=MK＞1，

∴S△MNK=NK×MP＞．

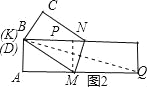
（3）如图2，当点B与点D重合时，△MNK的面积最大；

由题意得：MK=MQ（设为λ），则AM=5-λ；

由勾股定理得：（5-λ）2+12=λ2，

解得：λ=2.6；由（1）知：

NK=MK=2.6，MP=1，

∴S△MNK=NK×MP =1.3．