
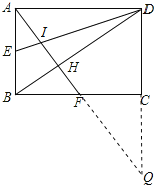
【题目】如图,已知矩形ABCD,AB=6,BC=8,E,F分别是AB,BC的中点,AF与DE相交于I,与BD相交于H,则四边形BEIH的面积为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
试题分析:延长AF交DC于Q点,由矩形的性质得出CD=AB=6,AB∥CD,AD∥BC,得出![]() =1,△AEI∽△QDE,因此CQ=AB=CD=6,△AEI的面积:△QDI的面积=3:12=1:4,∵AD=8,求出△AEI的面积=
=1,△AEI∽△QDE,因此CQ=AB=CD=6,△AEI的面积:△QDI的面积=3:12=1:4,∵AD=8,求出△AEI的面积=![]() ,△ABF的面积=12,△BFH的面积=4,四边形BEIH的面积=△ABF的面积﹣△AEI的面积﹣△BFH的面积,即可得出结果.
,△ABF的面积=12,△BFH的面积=4,四边形BEIH的面积=△ABF的面积﹣△AEI的面积﹣△BFH的面积,即可得出结果.
解:延长AF交DC于Q点,如图所示:
∵E,F分别是AB,BC的中点,
∴AE=![]() AB=3,BF=CF=
AB=3,BF=CF=![]() BC=4,
BC=4,
∵四边形ABCD是矩形,
∴CD=AB=6,AB∥CD,AD∥BC,
∴![]() =1,△AEI∽△QDE,
=1,△AEI∽△QDE,
∴CQ=AB=CD=6,△AEI的面积:△QDI的面积=3:12=1:4,
∵AD=8,
∴△AEI中AE边上的高=![]() ,
,
∴△AEI的面积=![]() ×3×
×3×![]() =
=![]() ,
,
∵△ABF的面积=![]() ×4×6=12,
×4×6=12,
∵AD∥BC,
∴△BFH∽△DAH,
∴![]() =
=![]() =
=![]() ,
,
∴△BFH的面积=![]() ×2×4=4,
×2×4=4,
∴四边形BEIH的面积=△ABF的面积﹣△AEI的面积﹣△BFH的面积=12﹣![]() ﹣4=
﹣4=![]() .
.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,A(0,4),C(3,0).
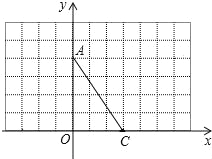
(1)①画出线段AC关于y轴对称线段AB;
②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;
(2)若直线y=kx平分(1)中四边形ABCD的面积,请直接写出实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(2)班组织了一次朗读比赛,甲、乙两队各10人的比赛成绩(10分制)如下表(单位:分):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队成绩的平均数和方差;
(3)已知甲队成绩的方差是1.4分2,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
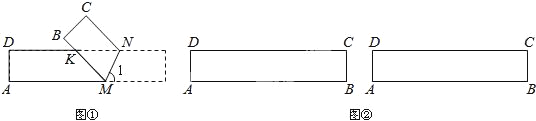
【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数
(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.
(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过 9 秒后边OC与边ON互相垂直.(直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一张矩形纸片![]() ,
, ![]() ,
, ![]() .在边
.在边![]() 上取一点
上取一点![]() ,在边
,在边![]() 上取一点
上取一点![]() ,将纸片沿
,将纸片沿![]() 折叠,使
折叠,使![]() 与
与![]() 交于点
交于点![]() ,得到
,得到![]() ,如图②所示.
,如图②所示.
(1)若![]() ,求
,求![]() 的度数.
的度数.
(2) ![]() 的面积能否小于
的面积能否小于![]() ?若能,求出此时
?若能,求出此时![]() 的度数;若不能,试说明理由.
的度数;若不能,试说明理由.
(3)如何折叠能够使![]() 的面积最大?请你画图探究可能出现的情况,求出最大值.
的面积最大?请你画图探究可能出现的情况,求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
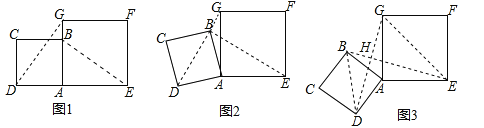
(1)小明发现![]() ,请你帮他说明理由.
,请你帮他说明理由.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.
(3)如图3,若小明将正方形ABCD绕点A继续逆时针旋转,顺次连接BD、DE、EG、GB,请你直接写出四边形BDEG面积的最大值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, A(0,4),B(-3,0).
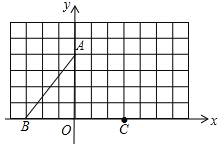
(1)①画出线段AB关于y轴对称线段AC;
②将线段AC绕点C顺时针旋转一个角,得到对应线段CD,使得AD//x轴,请画出线段CD;
(2)判断四边形ABCD的形状 ;
(3)若直线![]() 平分四边形ABCD的面积,请直接写出实数k的值.
平分四边形ABCD的面积,请直接写出实数k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com