Question

【题目】在数学兴趣小组活动中，小明进行数学探究活动．将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．

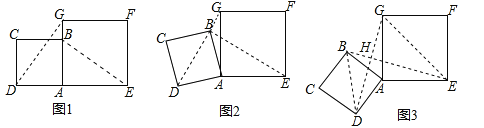
（1）小明发现，请你帮他说明理由．

（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时△ADG的面积．

（3）如图3，若小明将正方形ABCD绕点A继续逆时针旋转，顺次连接BD、DE、EG、GB，请你直接写出四边形BDEG面积的最大值 ．

Answer 1

【答案】（1）理由见解析；（2）1+；（3）．

【解析】

试题分析：（1）利用正方形得到条件，判断出△ADG≌△ABE从而∠AEB+∠ADG=90°，即可；

（2）利用正方形的性质在Rt△AMD中，∠MDA=45°，AD=2从而得出AM=DM=，在Rt△AMG中，AM2+GM2=AG2从而得出GM=即可；

（3）利用旋转，设旋转角为α，在Rt△AIB中，BI=ABsinα，在Rt△AHD中，DH=ADsinα，从而S四边形BDEG用sinα，即可．

试题解析：（1）如图1，延长EB交DG于点H

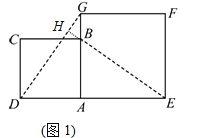
∵四边形ABCD与四边形AEFG是正方形

∴AD=AB，∠DAG=∠BAE=90°，AG=AE

∴△ADG≌△ABE（SAS）

∴∠AGD=∠AEB

∵△ADG中∠AGD+∠ADG=90°

∴∠AEB+∠ADG=90°

∵△DEH中，∠AEB+∠ADG+∠DHE=180°

∴∠DHE=90°

∴DG⊥BE．

（2）如图2，过点A作AM⊥DG交DG于点M，

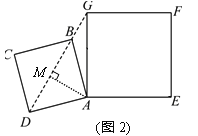
∠AMD=∠AMG=90°

∵BD是正方形ABCD的对角

∴∠MDA=45°

在Rt△AMD中，

∵∠MDA=45°，AD=2

∴AM=DM=在Rt△AMG中，

∵AM2+GM2=AG2

∴GM=

∵DG=DM+GM=+

∴S△ADG=DGAM=（+）×=1+

（3）如图3，

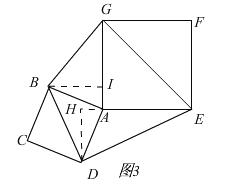
作DH⊥AE交EA的延长线与H，作BI⊥AG，

∵四边形ABCD是边长为2的正方形，

∴AB=AD=2，

设旋转角为α，

∴∠BIG=α，∠HAD=α，

在Rt△AIB中，BI=ABsinα，

在Rt△AHD中，DH=ADsinα，

∵四边形AEFG是边长为3的正方形，

∴AG=AE=3，

∴S/span>四边形BDEG=S△ABG+S△ABD+S△ADE+S△AEG

=S△ABD+S△AEG+S△ABG+S△ADE

=AB×AD+AG×AE+×AG×BI+AE×DH

=AB×AD+AG×AE+×AG×ABsinα+AE×ADsinα

=×2×2+×3×3+×3×2sinα+×3×2sinα

=+6sinα

当sinα=1时，S四边形BDEG最大，S四边形BDEG最大=．