
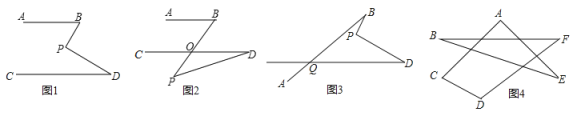
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若![]() ,点
,点![]() 在
在![]() 、
、![]() 内部,
内部,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,在AB∥CD的前提下,将点![]() 移到
移到![]() 、
、![]() 外部,则
外部,则![]() 、
、![]() 、
、![]() 之间有何数量关系?请证明你的结论.
之间有何数量关系?请证明你的结论.
(3)如图3,写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系?(不需证明)
之间的数量关系?(不需证明)
(4)如图4,求出![]() 的度数.
的度数.
【答案】(1)80°;(2)∠B=∠D+∠BPD,证明见解析;(3)∠BPD=∠B+∠D+BQD;;(4)360°.
【解析】
(1)过P作平行于AB的直线,根据内错角相等可得出三个角的关系,然后将∠B=50°,∠D=30°代入,即可求∠BPD的度数;
(2)先由平行线的性质得到∠B=∠BOD,然后根据∠BOD是三角形OPD的一个外角,由此可得出三个角的关系;
(3)延长BP交QD于M,再根据三角形的一个外角等于与它不相邻的两个内角的和解答;
(4)根据三角形外角性质得出∠CMN=∠A+∠E,∠DNB=∠B+∠F,代入∠C+∠D+CMN+∠DNM=360°即可求出答案.
(1)如图1,过P点作PO∥AB,
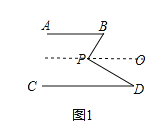
∵AB∥CD,∴CD∥PO∥AB,
∴∠BPO=∠B,∠OPD=∠D,
∵∠BPD=∠BPO+∠OPD,
∴∠BPD=∠B+∠D.
∵∠B=50°,∠D=30°,
∴∠BPD=∠B+∠D=50°+30°=80°;
(2)∠B=∠D+∠BPD,
∵AB∥CD,
∴∠B=∠BOD,
∵∠BOD=∠D+∠BPD,
∴∠B=∠D+∠BPD;
(3)如图:延长BP交QD于M
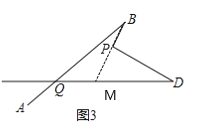
在△QBM中:∠BMD=∠BQD+∠QBM
在△PMD中:∠BPD=∠BMD+∠D=∠BQD+∠QBM+∠D
故答案为:∠BPD=∠B+∠D+BQD
∴![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系为:∠BPD=∠B+∠D+BQD
之间的数量关系为:∠BPD=∠B+∠D+BQD
(4)如图
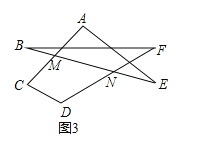
∵∠CMN=∠A+∠E,∠DNB=∠B+∠F,
又∵∠C+∠D+∠CMN+∠DNM=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
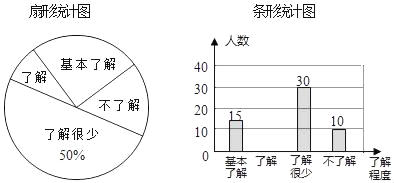
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 °;
(2)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为 人;
(3)若从对校园安全知识达到“了解”程度的3个女生A、B、C和2个男生M、N中分别随机抽取1人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到女生A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
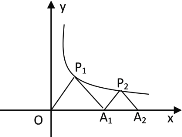
【题目】如图,ΔP1OA1,ΔP2A1A2是等腰直角三角形,点P1、P2在函数y=![]() (x>0)的图象上,斜边OA1、A1A2都在x轴上,则点A2的坐标是____________.
(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点A2的坐标是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
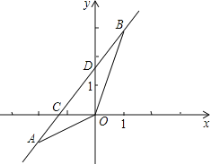
【题目】如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.
(1)求一次函数的解析式;
(2)求点C和点D的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密码锁有三个转轮,每个转轮上有十个数字:0,1,2,…9.小黄同学是9月份中旬出生,用生日“月份+日期”设置密码:9××
小张同学要破解其密码:
(1)第一个转轮设置的数字是9,第二个转轮设置的数字可能是 .
(2)请你帮小张同学列举出所有可能的密码,并求密码数能被3整除的概率;
(3)小张同学是6月份出生,根据(1)(2)的规律,请你推算用小张生日设置的密码的所有可能个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,D是BC的中点,以AC为腰向外作等腰直角△ACE,∠EAC=90°,连接BE,交AD于点F,交AC于点G.
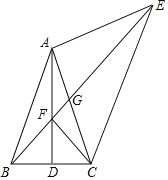
(1)若∠BAC=50°,求∠AEB的度数;
(2)求证:∠AEB=∠ACF;
(3)试判断线段EF、BF与AC三者之间的等量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
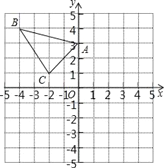
【题目】△ABC在直角坐标系内的位置如图所示.
(1)分别写出A、B、C的坐标;
(2)请在这个坐标系内画出△A1B1C1,使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标;
(3)请在这个坐标系内画出△A2B2C2,使△A2B2C2与△ABC关于原点对称,并写出A2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
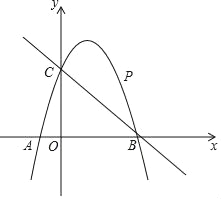
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com