
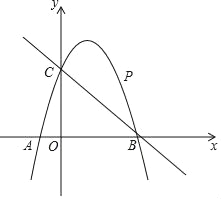
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
【答案】(1)y=﹣x2+2x+3(2)(![]() ,
,![]() )(3)当点P的坐标为(
)(3)当点P的坐标为(![]() ,
,![]() )时,四边形ACPB的最大面积值为
)时,四边形ACPB的最大面积值为![]()
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据菱形的对角线互相垂直且平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得P点坐标;
(3)根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得PQ的长,根据面积的和差,可得二次函数,根据二次函数的性质,可得答案.
(1)将点B和点C的坐标代入函数解析式,得
![]()
解得![]()
二次函数的解析式为y=﹣x2+2x+3;
(2)若四边形POP′C为菱形,则点P在线段CO的垂直平分线上,
如图1,连接PP′,则PE⊥CO,垂足为E,
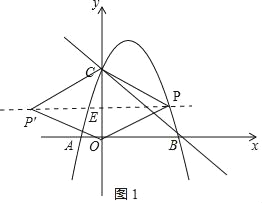
∵C(0,3),
∴![]()
∴点P的纵坐标![]() ,
,
当![]() 时,即
时,即![]()
解得![]() (不合题意,舍),
(不合题意,舍),
∴点P的坐标为![]()
(3)如图2,
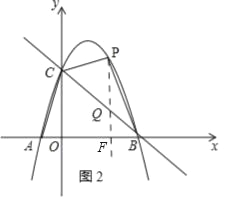
P在抛物线上,设P(m,﹣m2+2m+3),
设直线BC的解析式为y=kx+b,
将点B和点C的坐标代入函数解析式,得
![]()
解得![]()
直线BC的解析为y=﹣x+3,
设点Q的坐标为(m,﹣m+3),
PQ=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m.
当y=0时,﹣x2+2x+3=0,
解得x1=﹣1,x2=3,
OA=1,
![]()
S四边形ABPC=S△ABC+S△PCQ+S△PBQ
![]()
![]()
![]()
当m=![]() 时,四边形ABPC的面积最大.
时,四边形ABPC的面积最大.
当m=![]() 时,
时,![]() ,即P点的坐标为
,即P点的坐标为![]()
当点P的坐标为![]() 时,四边形ACPB的最大面积值为
时,四边形ACPB的最大面积值为![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若![]() ,点
,点![]() 在
在![]() 、
、![]() 内部,
内部,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,在AB∥CD的前提下,将点![]() 移到
移到![]() 、
、![]() 外部,则
外部,则![]() 、
、![]() 、
、![]() 之间有何数量关系?请证明你的结论.
之间有何数量关系?请证明你的结论.
(3)如图3,写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系?(不需证明)
之间的数量关系?(不需证明)
(4)如图4,求出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC在平面直角坐标系中的位置如图所示,已知![]() ,点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作
,点A在x轴上,点C在y轴上,P是对角线OB上一动点(不与原点重合),连接PC,过点P作![]() ,交x轴于点D.下列结论:①
,交x轴于点D.下列结论:①![]() ;②当点D运动到OA的中点处时,
;②当点D运动到OA的中点处时,![]() ;③在运动过程中,
;③在运动过程中,![]() 是一个定值;④当△ODP为等腰三角形时,点D的坐标为
是一个定值;④当△ODP为等腰三角形时,点D的坐标为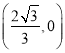 .其中正确结论的个数是( )
.其中正确结论的个数是( )
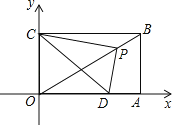
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
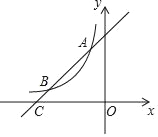
【题目】如图,一次函数y=x+4的图象与反比例函数y=![]() (k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(k为常数且k≠0)的图象交于A(﹣1,a),B两点,与x轴交于点C.
(1)求此反比例函数的表达式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班数学老师将本班某次参加的数学竞赛成绩(得分取整数,满分100分)进行整理统计后,制成如下的频数直方图和扇形统计图,请根据统计图提供的信息,解答下列问题:
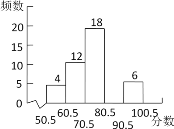
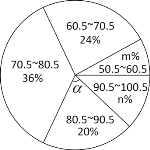
(1)在分数段70.5~80.5分的频数、频率分别是多少?
(2)m、n、![]() 的值分别是多少?
的值分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
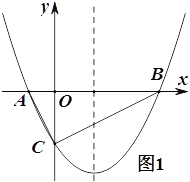
【题目】如图,已知抛物线![]() (
(![]() >0)与
>0)与![]() 轴交于A,B两点(A点在B点的左边),与
轴交于A,B两点(A点在B点的左边),与![]() 轴交于点C。
轴交于点C。
(1)如图1,若△ABC为直角三角形,求![]() 的值;
的值;
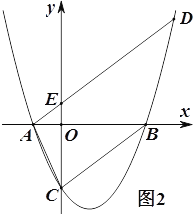
(2)如图1,在(1)的条件下,点P在抛物线上,点Q在抛物线的对称轴上,若以BC为边,以点B,C,P,Q为顶点的四边形是平行四边形,求P点的坐标;
(3)如图2,过点A作直线BC的平行线交抛物线于另一点D,交![]() 轴交于点E,若AE:ED=1:4,求
轴交于点E,若AE:ED=1:4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
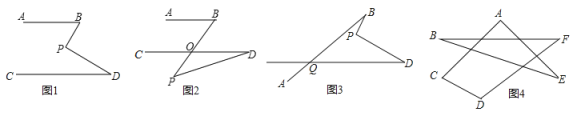
【题目】如图所示,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )

A.带①去B.带②去C.带③去D.带①和②去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com