
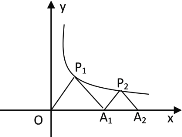
【题目】如图,ΔP1OA1,ΔP2A1A2是等腰直角三角形,点P1、P2在函数y=![]() (x>0)的图象上,斜边OA1、A1A2都在x轴上,则点A2的坐标是____________.
(x>0)的图象上,斜边OA1、A1A2都在x轴上,则点A2的坐标是____________.
【答案】(4![]() ,0)
,0)
【解析】
首先根据等腰直角三角形的性质,知点P1的横、纵坐标相等,再结合双曲线的解析式得到点P1的坐标是(2,2),则根据等腰三角形的三线合一求得点A1的坐标;同样根据等腰直角三角形的性质、点A1的坐标和双曲线的解析式求得A2点的坐标.
根据等腰直角三角形的性质,可设点P1(a,a),
又∵y=![]() ,∴a2=4,a=±2(负值舍去),
,∴a2=4,a=±2(负值舍去),
再根据等腰三角形的三线合一,得A1的坐标是(4,0),
设点P2的坐标是(4+b,b),又∵y=![]() ,则b(4+b)=4,
,则b(4+b)=4,
即b2+4b4=0,
又∵b>0,∴b=2![]() 2,
2,
再根据等腰三角形的三线合一,
∴4+2b=4+4![]() 4=4
4=4![]() ,
,
∴点A2的坐标是(4![]() ,0).
,0).


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O直径,⊙O过AC的中点D,DE⊥BC,垂足为E.
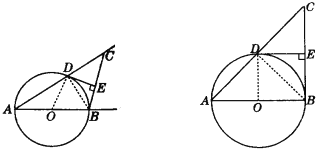
(1)由这些条件,你能得出哪些结论?(要求:不准标其他字母,找结论过程中所连的辅助线不能出现在结论中,不写推理过程,写出4个结论即可)
(2)若∠ABC为直角,其他条件不变,除上述结论外你还能推出哪些新的正确结论?并画出图形.(要求:写出6个结论即可,其他要求同(1))
查看答案和解析>>
科目:初中数学 来源: 题型:
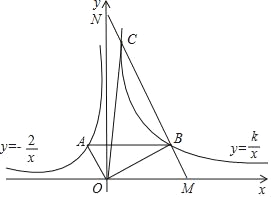
【题目】如图,∠AOB=90°,反比例函数y=﹣![]() (x<0)的图象过点A(﹣1,a),反比例函数y=
(x<0)的图象过点A(﹣1,a),反比例函数y=![]() (k>0,x>0)的图象过点B,且AB∥x轴.
(k>0,x>0)的图象过点B,且AB∥x轴.
(1)求a和k的值;
(2)过点B作MN∥OA,交x轴于点M,交y轴于点N,交双曲线y=![]() 于另一点C,求△OBC的面积.
于另一点C,求△OBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
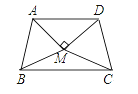
【题目】如图,![]() 与
与![]() 是两个全等的等边三角形,
是两个全等的等边三角形,![]() .有下列四个结论:①
.有下列四个结论:①![]() ;②
;②![]() ;③直线
;③直线![]() 垂直平分线段
垂直平分线段![]() ;④四边形
;④四边形![]() 是轴对称图形.其中正确的结论有_____.(把正确结论的序号填在横线上)
是轴对称图形.其中正确的结论有_____.(把正确结论的序号填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差(分2) | |
初中部 | a | 85 | b | s初中2 |
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差s初中2,并判断哪一个代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,菱形ABCD的边AB在x轴上,已知点A(2,0),点C(10,4),双曲线经过点D.
(1)求菱形ABCD的边长;
(2)求双曲线的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
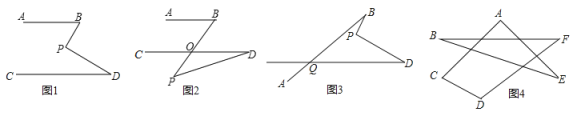
【题目】平面内的两条直线有相交和平行两种位置关系.
(1)如图1,若![]() ,点
,点![]() 在
在![]() 、
、![]() 内部,
内部,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
(2)如图2,在AB∥CD的前提下,将点![]() 移到
移到![]() 、
、![]() 外部,则
外部,则![]() 、
、![]() 、
、![]() 之间有何数量关系?请证明你的结论.
之间有何数量关系?请证明你的结论.
(3)如图3,写出![]() 、
、![]() 、
、![]() 、
、![]() 之间的数量关系?(不需证明)
之间的数量关系?(不需证明)
(4)如图4,求出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
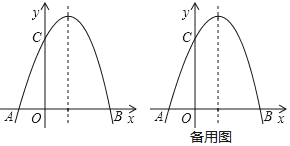
【题目】已知,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和C(0,3).(1)求抛物线的解析式;(2)在抛物线的对称轴上,是否存在点P,使PA+PC的值最小?如果存在,请求出点P的坐标,如果不存在,请说明理由;(3)设点M在抛物线的对称轴上,当△MAC是直角三角形时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com