【题目】如图，平面直角坐标系中，菱形ABCD的边AB在x轴上，已知点A(2，0)，点C(10，4)，双曲线经过点D.

(1)求菱形ABCD的边长；

(2)求双曲线的解析式．

参考答案：

【答案】(1)5；(2).

【解析】试题分析：过点C作CE⊥AB于点E，设菱形的边长为，则 在中，利用勾股定理建立关于的方程，解方程求出的值即可.

设双曲线的解析式为，过点D作DF⊥AB于点F，分别求出的长，则点D的坐标可知，代入双曲线的解析式求出的值即可．

试题解析：(1)设菱形的边长为x，则BC＝AB＝x.

如图，过点C作CE⊥AB于点E.

∵点A的坐标为(2，0)，点C的坐标为(10，4)，

∴OA＝2，CE＝4，OE＝10，

∴BE＝OE－OA－AB＝10－2－x.

在Rt△BEC中，由勾股定理可得BC2＝BE2＋CE2，

即x2＝(10－2－x)2＋42，

解得x＝5，

∴菱形ABCD的边长为5.

(2)设双曲线的解析式.如图，过点D作DF⊥AB于点F，

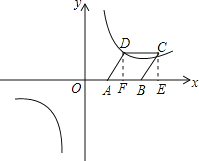
则DF＝CE＝4，EF＝CD＝5，

∴OF＝OE－EF＝10－5＝5，

∴点D的坐标为(5，4)，

∴k＝20，

∴双曲线的解析式为

关闭