
【题目】如图,在![]() 中,
中,![]() ,过点
,过点![]() 的直线
的直线![]() ,
,![]() 为
为![]() 边上一点,过点
边上一点,过点![]() 作
作![]() 于
于![]() ,交直线
,交直线![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 在
在![]() 中点时,四边形
中点时,四边形![]() 是什么特殊四边形?说明你的理由;
是什么特殊四边形?说明你的理由;
(3)若![]() 为
为![]() 中点,则当
中点,则当![]() ______度时,四边形
______度时,四边形![]() 是正方形.
是正方形.
 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|.
利用数轴,根据数形结合思想,回答下列问题:
![]()
(1)已知|x|=3,则x的值是 .
(2)数轴上表示2和6两点之间的距离是 ,数轴上表示1和﹣2的两点之间的距离为 ;
(3)数轴上表示x和1两点之间的距离为 ,数轴上表示x和﹣3两点之间的距离为
(4)若x表示一个实数,且﹣5<x<3,化简|x﹣3|+|x+5|= ;
(5)|x+3|+|x﹣4|的最小值为 ,|x﹣1|+|x﹣2|+|x﹣3|+|x﹣4|+|x﹣5|的最小值为 .
(6)|x+1|﹣|x﹣3|的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
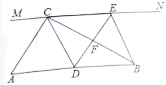
【题目】已知:如图,C是AB上一点,点D,E分别在AB两侧,AD∥BE,且AD=BC,BE=AC.

(1)求证:CD=CE;
(2)连接DE,交AB于点F,猜想△BEF的形状,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点B,D表示的数互为相反数,那么图中点A、点D表示的数分别是 、 ;
(2)当点B为原点时,在数轴上是否存在点M,使得点M到点A的距离是点M到点D的距离的2倍,若存在,请求出此时点M所表示的数;若不存在,说明理由;
(3) 在(2)的条件下,点A、点C分别以2个单位长度/秒和0.5个单位长度同时向右运动,同时点P从原点出发以3个单位长度/秒的速度向左运动,当点A与点C之间的距离为3个单位长度时,求点P所对应的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“幸福是奋斗出来的”,在数轴上,若C到A的距离刚好是3,则C点叫做A的“幸福点”,若C到A、B的距离之和为6,则C叫做A、B的“幸福中心”
(1)如图1,点A表示的数为﹣1,则A的幸福点C所表示的数应该是 ;
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2,点C就是M、N的幸福中心,则C所表示的数可以是 (填一个即可);
(3)如图3,A、B、P为数轴上三点,点A所表示的数为﹣1,点B所表示的数为4,点P所表示的数为8,现有一只电子蚂蚁从点P出发,以2个单位每秒的速度向左运动,当经过多少秒时,电子蚂蚁是A和B的幸福中心?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为培养学生的特长爱好,提高学生的综合素质,某校音乐特色学习斑准备从京东商城里一次性购买若干个尤克里里和竖笛(每个尤克里里的价格相同,每个竖笛的价格相同),购买![]() 个竖笛和
个竖笛和![]() 个尤克里里共需
个尤克里里共需![]() 元;竖笛单价比尤克里里单价的一半少
元;竖笛单价比尤克里里单价的一半少![]() 元.
元.
(1)求竖笛和尤克里里的单价各是多少元?
(2)根据学校实际情况,需一次性购买竖笛和尤克里里共![]() 个,但要求购买竖笛和尤克里里的总费用不超过
个,但要求购买竖笛和尤克里里的总费用不超过![]() 元,则该校最多可以购买多少个尤克里里?
元,则该校最多可以购买多少个尤克里里?
查看答案和解析>>
科目:初中数学 来源: 题型:
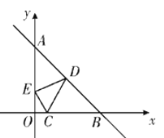
【题目】如图所示,已知点C(1,0),直线![]() 与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是( )
A.![]() B.10
B.10
C.![]() D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园有一片长方形竹林,栽了25棵竹子,为了方便管理,每个竹子都有自己的编号,如图所示.标有2、3、5、7、10、13、17、21的竹子都在拐角处,如果![]() 处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )
处也栽一棵竹子,编号为26,在此转弯(如虚线),按以上规律继续栽竹子,则第200个拐角处编号2在第1个拐角处)的竹子的编号应为( )

A.10010B.10101
C.10100D.10110
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com