
【题目】下列运算正确的是( )
A.a3+a4=a7
B.2a3a4=2a7
C.(2a4)3=8a7
D.a8÷a2=a4
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成![]() 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究![]() 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当![]() 时,
时,![]()
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当![]() 时,
时,![]()
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
综上所述,可得表①
| 3 | 4] | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2)分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三
角形?(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用![]() 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】提出问题:当x>0时如何求函数y=x+![]() 的最大值或最小值?
的最大值或最小值?
分析问题:前面我们刚刚学过二次函数的相关知识,知道求二次函数的最值时,我们可以利用它的图象进行猜想最值,或利用配方可以求出它的最值.
例如我们求函数y=x﹣2![]() (x>0)的最值时,就可以仿照二次函数利用配方求最值的方法解决问题;y=x﹣2
(x>0)的最值时,就可以仿照二次函数利用配方求最值的方法解决问题;y=x﹣2![]() =(
=(![]() )2﹣2
)2﹣2![]() ﹣2
﹣2![]() +1﹣1=(
+1﹣1=(![]() ﹣1)2﹣1即当x=1时,y有最小值为﹣1
﹣1)2﹣1即当x=1时,y有最小值为﹣1
解决问题
借鉴我们已有的研究函数的经验,探索函数y=x+![]() (x>0)的最大(小)值.
(x>0)的最大(小)值.
(1)实践操作:填写下表,并用描点法画出函数y=x+![]() (x>0)的图象:
(x>0)的图象:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … | … |
(2)观察猜想:观察该函数的图象,猜想
当x= 时,函数y=x+![]() (x>0)有最 值(填“大”或“小”),是 .
(x>0)有最 值(填“大”或“小”),是 .
(3)推理论证:利用上述例题,请你尝试通过配方法求函数y=x+![]() (x>0)的最大(小)值,以证明你的猜想.知识能力运用:直接写出函数y=﹣2x﹣
(x>0)的最大(小)值,以证明你的猜想.知识能力运用:直接写出函数y=﹣2x﹣![]() (x>0)当x= 时,该函数有最 值(填“大”或“小”),是 .
(x>0)当x= 时,该函数有最 值(填“大”或“小”),是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,菱形ABCD中,CH⊥AB,垂足为H,交对角线AC于M,连接BM,且AH=3.
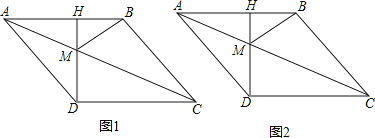
(1)求DM的长;
(2)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(3)在(2)的条件下,当点P在边AB上运动时,是否存在这样的t的值,使∠MPB与∠BCD互为余角?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com