
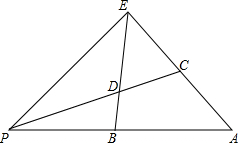
 如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE.
如图所示,在△PEA中,B是边PA上一点,∠PEB=∠A,过点P的直线分别交EB,EA于点D,C,且ED=EC,试说明:PA•CE=AC•PE. 科目:初中数学 来源: 题型:填空题
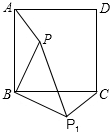 如图,点P是正方形ABCD内一点,将△ABP绕点B按顺时针方向旋转至与△CBP1重合,若PB=4cm,则PP1=4$\sqrt{2}$cm.
如图,点P是正方形ABCD内一点,将△ABP绕点B按顺时针方向旋转至与△CBP1重合,若PB=4cm,则PP1=4$\sqrt{2}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
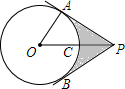 如图,PA,PB分别与⊙O相切于A,B两点,PO交⊙O于点C,PC=OC,AP=4$\sqrt{3}$cm.
如图,PA,PB分别与⊙O相切于A,B两点,PO交⊙O于点C,PC=OC,AP=4$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
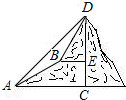 已知:如图,在山脚的A处测得山顶D的仰角为45°,沿着坡度为30°的斜角前进400米处到B处(即∠BAC=30°,AB=400米),测得D的仰角为60°,求山的高度CD.
已知:如图,在山脚的A处测得山顶D的仰角为45°,沿着坡度为30°的斜角前进400米处到B处(即∠BAC=30°,AB=400米),测得D的仰角为60°,求山的高度CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 队名 | 比赛场次 | 胜场 | 负场 | 积分 |
| 前进 | 14 | 10 | 4 | 24 |
| 东方 | 10 | 4 | 4 | 24 |
| 光明 | 14 | 9 | 5 | 23 |
| 蓝天 | 14 | 9 | 5 | 23 |
| 雄鹰 | 14 | 7 | 7 | 21 |
| 远大 | 14 | 7 | 7 | 21 |
| 卫星 | 14 | 4 | 10 | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com