
����Ŀ�� �Ķ����ϣ�
Ϊ��ʵˮ��Դ�����ƶȣ������ٽ�ˮ��Դ��Լ�����о�����ˮʵ�н���ˮ�ۣ��������ˮ�����㣬�������ͥȫ����ˮ������Ϊ������ˮ�۷ֵ�������ʵʩϸ�������

��ij������ȥ����ˮ��Ϊ190�����ף�����Ӧ����ˮ��Ϊ180��5+(190��180)��7=970Ԫ��
(1)��С����ȥ����ˮ��Ϊ100�����ף���С����Ӧ���ɵ�ˮ��Ϊ________Ԫ��
(2)����ֹ10�µף�С���ҽ��깲��ˮ��1145Ԫ����С���ҹ���ˮ_______�����ף�
(3)��С����ȫ����ˮ��x������270�����ף���Ӧ���ɵ�ˮ��Ϊ����Ԫ��(�ú�x�Ĵ���ʽ��ʾ)
���𰸡�(1)500��(2)215 ��(3)��0��x��180ʱ��ˮ��Ϊ5x Ԫ����180��x��260ʱ��ˮ��Ϊ��7x��360��Ԫ����260��x��270ʱ��ˮ��Ϊ��9x��880��Ԫ.
��������
��1����ˮ��Ϊ100�����ף����ڵ�һ���ݣ�����5Ԫ/�������㼴�ɣ�
��2������ˮ����180������ʱ��ˮ��Ϊ180��5=900Ԫ������ˮ����260������ʱ��ˮ��Ϊ180��5+(260��180)��7=1460Ԫ����С���ҽ��깲��ˮ��1145Ԫ���ж���ˮ����180������260������֮�䣬����ˮ��x�����ף����з��� 180��5+(x��180)��7=1145���ⷽ�̼���.
��3��������������ۣ���0��x��180ʱ����180��x��260ʱ����260��x��270ʱ���ֱ���ˮ�۱��г�����ʽ����.
��1������ˮ��Ϊ100�����ף����ڵ�һ����,
��ˮ��Ϊ100��5=500Ԫ.
��2����С���ҽ��깲��ˮ��1145Ԫ���ж���ˮ����180������260������֮�䣬����ˮ��x�����ף��������180��5+(x��180)��7=1145�����x=215.
����ˮ��Ϊ215������.
��3����0��x��180ʱ��ˮ��Ϊ5xԪ��
��180��x��260ʱ��ˮ��Ϊ180��5+(x��180)��7=��7x��360��Ԫ;
��260��x��270ʱ��ˮ��Ϊ180��5+(260��180)��7+(x��260)��9=��9x��880��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ��ɽ���ǽ�ɽ��ɽ����Ϊ������̬������A��B������������������������������Ͳ������䣬ÿ��μ������������ܿ�֧���±���
��ׯ | ����������������/�� | ����������������/�� | ��֧��/Ԫ |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
��1������������ͬ����ߵ��˾�֧������һ������������������Ͳ���������˾�֧�����ø��Ƕ���Ԫ��
��2�����˾�֧�����ò��������£�Ϊ��Լ��֧�����������40�˹�ͬ������������Ͳ������䣬Ҫʹ��֧��������102000Ԫ��������������������С�������������������������ļ��ַ���������Ա������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��������ȤС������ͼ����ʾ�ľ��γ����Ͽ�չѵ���������˴ӵ�A�������ھ���ABCD��������A��B��C��D�ķ��������ƶ��������Dʱֹͣ�ƶ�����֪AD=6����λ���ȣ������˵��ٶ�Ϊ1����λ����/s�����ƶ����սǴ�������������ʱ����Բ��ƣ������������ʱ��Ϊt��s��ʱ��������λ���õ�P��ʾ��P���Խ���BD�ľ��루�����߶�PQ�ij���Ϊd����λ���ȣ�����d��t�ĺ���ͼ����ͼ����ʾ��
��1��ͼ���к���ͼ��������Ľ����������![]() ��ͼ���б�ʾһ���߶εij�������ͼ���л��������߶Σ�
��ͼ���б�ʾһ���߶εij�������ͼ���л��������߶Σ�
��2����ͼ����a��ֵ��
��3����ͼ������M��N�ֱ����߶�EF��GH�ϣ��߶�MNƽ���ں��ᣬM��N�ĺ�����ֱ�Ϊt1��t2�������������t1��s�������P1��������t2��s�������P2������ͼ��������CP1+CP2=7����t1��t2��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����κ���ͼ���ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ�����ʾ��
�Ķ�Ӧֵ�����ʾ��
| �� | ��3 | ��2 | ��1 | 0 | 1 | �� |
| �� | 0 | ��3 | ��4 | ��3 | 0 | �� |
(1)��������κ����ı���ʽ��
(2)�ڸ�����ƽ��ֱ������ϵ�л���������κ�����ͼ��
(3)��![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]()
![]()
![]() ������Ϊ
������Ϊ![]() ����
����![]() �ġ�O�ֱ���
�ġ�O�ֱ���![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��
��1����֤��![]() ��
��![]() ��
��
��2����![]() ���O����ʱ�����O�������
���O����ʱ�����O�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
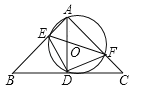
����Ŀ����֪����ͼ����1����2����3����E����˵������A����EBC�����밴ͼ��գ���������.��
֤�����ߡ�1����2 (��֪)��

��________��_______( )��
���E����_______ ( )��
���ߡ�E����3 (��֪)��
���3����____________ ( �������� )��
��_________��________ (�ڴ�����ȣ���ֱ��ƽ��),
���A����EBC ( )��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڷ���ֽ�У��������߶�AB��BC���÷���ֽ������²�����������ͼ�ۼ�����
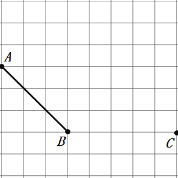
��1������A��BC��ƽ���ߣ�
��2������C��AB��ƽ���ߣ��루1���е�ƽ���߽��ڵ�D��
��3������B��AB�Ĵ��ߣ��루1���е�ƽ���߽��ڵ�F.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и��������ȷ���� ( )
A. (ab��1)��(��4ab2)=��4a2b3��4ab2 B. (3x2+xy��y2)��3x2=9x4+3x3y��y2
C. (��3a)��(a2��2a+1)=��3a3+6a2 D. (��2x)��(3x2��4x��2)=��6x3+8x2+4x
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com