
【题目】已知:关于![]() 的方程
的方程![]() .
.
(1)若这个方程有两个不相等的实数根,求![]() 的取值范围;
的取值范围;
(2)若此方程有一个根是1,求![]() 的值.
的值.
【答案】(1)k>-1;(2)k的值为5.
【解析】
(1)根据方程有两个不相等的实数根,即可得出△=[-2(k+2)]2-4(k2-2k-2)=24k+24>0,解之即可得出k的取值范围;
(2)将x=1代入原方程,解之即可求出k值.
解:(1)∵关于x的方程x2-2(k+2)x+k2-2k-2=0有两个不相等的实数根,
∴△=[-2(k+2)]2-4(k2-2k-2)=24k+24>0,
解得:k>-1. 故k的取值范围是k>-1;
(2)将x=1代入原方程得1-2(k+2)+k2-2k-2=k2-4k-5=(k+1)(k-5)=0,
解得:k1=-1(舍去),k2=5.
所以k的值为5.


科目:初中数学 来源: 题型:
【题目】如图,把6张长为a、宽为b(a>b)的小长方形纸片不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设这两个长方形的面积的差为S.当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b满足( )

A. a=1.5bB. a=2.5bC. a=3bD. a=2b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是边CD上一点(点E不与点C、D重合),连结BE.
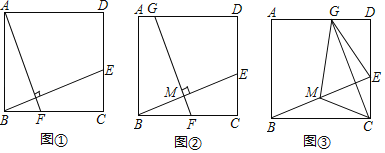
(感知)如图①,过点A作AF⊥BE交BC于点F.易证△ABF≌△BCE.(不需要证明)
(探究)如图②,取BE的中点M,过点M作FG⊥BE交BC于点F,交AD于点G.
(1)求证:BE=FG.
(2)连结CM,若CM=1,则FG的长为 .
(应用)如图③,取BE的中点M,连结CM.过点C作CG⊥BE交AD于点G,连结EG、MG.若CM=3,则四边形GMCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:

(1)李大爷自带的零钱是多少?
(2)降价前他每千克黄瓜出售的价格是多少?
(3)卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,问他一共批发了多少千克的黄瓜?
(4)请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程的解法中,错误的个数是( )
①方程2x-1=x+1移项,得3x=0
②方程![]() =1去分母,得x-1=3=x=4
=1去分母,得x-1=3=x=4
③方程1-![]() 去分母,得4-x-2=2(x-1)
去分母,得4-x-2=2(x-1)
④方程![]() 去分母,得2x-2+10-5x=1
去分母,得2x-2+10-5x=1
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,∠1+∠2=230°,b∥c,则∠1,∠2,∠3,∠4各是多少度?
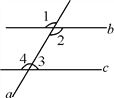
解:∵∠1=∠2(__________________),
∠1+∠2=230°,
∴∠1=∠2=___________(填度数).
∵b∥c,
∴∠4=∠2=_______(填度数)(_______________________________),
∠2+∠3=180°(________________________________),
∴∠3=180°-∠2=____________(填度数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师从咸宁出发到外地参加教育信息化应用技术提高培训,他可以乘坐普通列车,也可以乘坐高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍.若高铁的平均速度(千米/小时)是普通列车平均速度的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间少3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)( )
≈1.732)( )
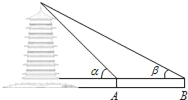
A. 36.21米 B. 37.71米 C. 40.98米 D. 42.48米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com