
【题目】已知:如图,正比例函数y=ax的图象与反比例函数y= ![]() 的图象交于点C(3,1)
的图象交于点C(3,1)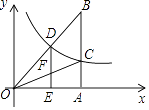
(1)试确定上述比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点D(m,n)是反比例函数图象上的一动点,其中0<m<3,过点C作直线AC⊥x轴于点A,交OD的延长线于点B;若点D是OB的中点,DE⊥x轴于点E,交OC于点F,试求四边形DFCB的面积.
【答案】
(1)解:将点C(3,1)分别代入y= ![]() 和y=ax,得:k=3,a=
和y=ax,得:k=3,a= ![]() ,
,
∴反比例函数解析式为y= ![]() ,正比例函数解析式为y=
,正比例函数解析式为y= ![]() x;
x;
(2)解:观察图象可知,在第二象限内,当0<x<3时,反比例函数值大于正比例函数值;
(3)解:∵点D(m,n)是OB的中点,又在反比例函数y= ![]() 上,
上,
∴OE= ![]() OA=
OA= ![]() ,点D(
,点D( ![]() ,2),
,2),
∴点B(3,4),
又∵点F在正比例函数y= ![]() x图象上,
x图象上,
∴F( ![]() ,
, ![]() ),
),
∴DF= ![]() 、BC=3、EA=
、BC=3、EA= ![]() ,
,
∴四边形DFCB的面积为 ![]() ×(
×( ![]() +3)×
+3)× ![]() =
= ![]() .
.
【解析】(1)利用待定系数法把C坐标代入解析式即可;(2)须数形结合,先找出交点,在交点的左侧与y轴之间,反比例函数值大于正比例函数值.(3)求出DF、BC、EA,代入梯形面积公式即可.


科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径,CD为⊙O的弦,CD∥AB,过点B的切线与射线AD交于点M,连接AC,BD.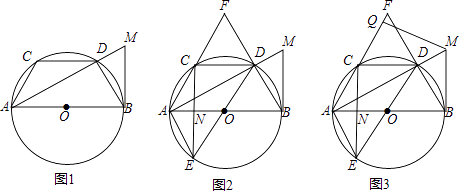
(1)如图l,求证:AC=BD;
(2)如图2,延长AC、BD交于点F,作直径DE,连接AE、CE,CE与AB交于点N,求证:∠AFB=2∠AEN;
(3)如图3,在(2)的条件下,过点M作MQ⊥AF于点Q,若MQ:QC=3:2,NE=2,求QF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
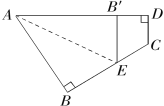
【题目】如图所示,一个四边形纸片ABCD,∠B=∠D=![]() ,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
,把纸片按如图所示折叠,使点B落在AD边上的B′点,AE是折痕.
(1)试判断B′E与DC的位置关系;并说明理由.
(2)如果∠C=![]() ,求∠AEB的度数.
,求∠AEB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
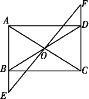
【题目】如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
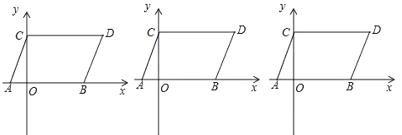
【题目】如图10,在平面直角坐标系中,点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,且
,且![]() 满足
满足![]() .现同时将点
.现同时将点![]() 分别向上平移2个单位,再向右平移1个单位,分别得到点
分别向上平移2个单位,再向右平移1个单位,分别得到点![]() 的对应点
的对应点![]() ,连接
,连接![]() 得
得![]() .
.
(1)直接写出点![]() 的坐标和四边形
的坐标和四边形![]() 的面积;
的面积;
(2)若在坐标轴上存在点![]() ,使
,使![]() 四边形
四边形![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)若点![]() 在直线
在直线![]() 上运动,连接
上运动,连接![]() .请画出图形,写出
.请画出图形,写出![]() 的数量关系并证明.
的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题.
用棋子摆成的“T”字形图如图所示:

(1)填写下表:
图形序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子个数 | 5 | 8 | … |
(2)写出第n个“T”字形图案中棋子的个数_________________(用含n的代数式表示);
(3)第20个“T”字形图案共有棋子____________个?
(4)计算前20个“T”字形图案中棋子的总个数.
(提示:请你先思考下列问题:第1个图案与第20个图案中共有多少个棋子?第2个图案与第19个图案中共有多少个棋子?第3个图案与第18个图案呢?)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N.下面是推理过程,请你填空:
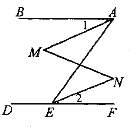
解:∵∠BAE+∠AED=180° (已知) ,
∴AB//DE( ),
∴∠BAE= ( )
又 ∵∠1=∠2(已知)
∴∠BAE-∠1= - (等式性质),
即∠MAE=∠NEA,
∴ ∥ ( ),
∴∠M=∠N(两直线平行,内错角相等).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com