
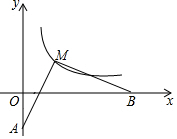
 如图,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,已知A(0,-1),B(5,0),若MA=MB,且MA⊥MB,求k的值.
如图,点M为双曲线y=$\frac{k}{x}$(x>0)上一点,已知A(0,-1),B(5,0),若MA=MB,且MA⊥MB,求k的值. 分析 先过M作MC⊥x轴于C,MD⊥y轴于D,构造全等三角形:△ADM≌△BCM,设正方形CODM的边长为a,根据全等三角形的对应边相等,即可得到关于a的方程,进而得到M的坐标,进而得出k的值.
解答 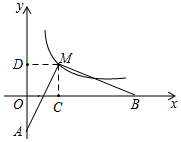 解:如图所示,过M作MC⊥x轴于C,MD⊥y轴于D,则∠DMC=90°=∠ADM=∠BCM,
解:如图所示,过M作MC⊥x轴于C,MD⊥y轴于D,则∠DMC=90°=∠ADM=∠BCM,
∵∠AMB=90°,
∴∠AMD=∠BMC,
在△ADM和△BCM中,
$\left\{\begin{array}{l}{∠ADM=∠BCM}\\{∠AMD=∠BMC}\\{AM=BM}\end{array}\right.$,
∴△ADM≌△BCM(AAS),
∴DM=CM,BC=AD,
∴四边形CODM是正方形,
设正方形CODM的边长为a,
∵A(0,-1),B(5,0),
∴BC=5-a,AD=a+1,
∴5-a=a+1,
解得a=2,
∴M(2,2),
∵点M为双曲线y=$\frac{k}{x}$(x>0)上一点,
∴k=2×2=4,
故k的值为4.
点评 本题主要考查了反比例函数图象上点的坐标特征以及全等三角形的判定与性质的运用,解决问题的关键是作辅助线构造全等三角形,依据等边三角形的对应边相等进行求解.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{(x-1)^{2}}$ | B. | $\frac{1}{x-1}$ | C. | $\frac{3}{x-1}$ | D. | $\frac{3}{x+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解西宁电视台“教育在线”栏目的收视率 | |
| B. | 了解青海湖斑头雁种群数量 | |
| C. | 了解全国快递包裹产生包装垃圾的数量 | |
| D. | 了解某班同学“跳绳”的成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 65×102 | B. | 6.5×102 | C. | 6.5×103 | D. | 6.5×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
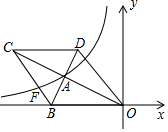 如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上反比例函数y=$\frac{k}{x}({x<0})$的图象经过菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(-6,8),则k的值为-32.
如图,在平面直角坐标系中,菱形OBCD的边OB在x轴负半轴上反比例函数y=$\frac{k}{x}({x<0})$的图象经过菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(-6,8),则k的值为-32.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
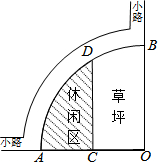 如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6m,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是( )| A. | $(6π-\frac{9}{2}\sqrt{3}){m^2}$ | B. | $(6π-9\sqrt{3}){m^2}$ | C. | $(π-\frac{9}{2}\sqrt{3}){m^2}$ | D. | $(10π-\frac{9}{2}\sqrt{3}){m^2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
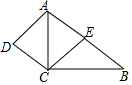 如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.
如图,在四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com