
分析 由y=(a+1)x2+ax+1的图象与x轴没有交点,依据根的判别式△=b2-4ac<0、联立二次项系数>0得出关于a的一元二次不等式组,解不等式组可得出a的取值范围;根据关于x的不等式组$\left\{\begin{array}{l}{x+2≥a}\\{1-x≥2a}\end{array}\right.$有解亦可得出a的取值范围;将两个条件合在一起结合题意,可知a只能为0或1,结合随机事件的概率公式即可得出结论.
解答 解:∵y=(a+1)x2+ax+1的图象与x轴没有交点,
∴$\left\{\begin{array}{l}{a+1>0}\\{{a}^{2}-4(a+1)<0}\end{array}\right.$,
解得:2-2$\sqrt{2}$<a<2+2$\sqrt{2}$.
解不等式组$\left\{\begin{array}{l}{x+2≥a}\\{1-x≥2a}\end{array}\right.$得:a≤1.
∴a的取值可以为0,1.
P=$\frac{2}{4}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了概率公式、解一元一次不等式组、抛物线与x轴的交点,解题的关键是解关于a的不等式组,得出a的取值范围.本题属于基础题,难度不大,解决该题型题目时,根据抛物线与x轴没有交点得出关于a的一元二次不等式组是关键.


科目:初中数学 来源:2017届江西省高安市九年级下学期第一次模拟考试数学试卷(解析版) 题型:填空题
2016年我市经济依然保持了平稳增长。据统计,截止到今年4月底,我市金融机构存款余额约为1193亿元,用科学计数法应记为_____________元
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:填空题
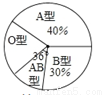
小明同学根据全班同学的血型绘制了如图所示的扇形统计图,已知A型血的有20人,则O型血的有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.
如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
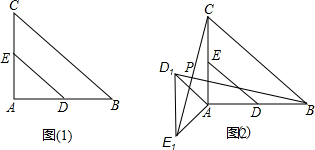 如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
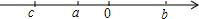 已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.
已知实数a,b,c关系是a<0,b>0,c<0,且|c|>|b|>|a|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
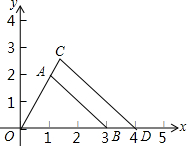 如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.
如图,△AOB以O为位似中心,扩大到△COD,各点的坐标分别为A(1,2),B(3,0),D(4,0),求点C的坐标,并求出四边形ABDC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
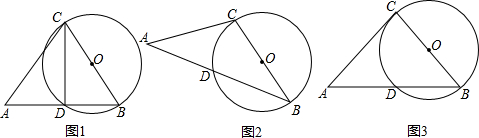
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com