
����Ŀ�����壺���������У���һ�ߵ��е㵽�����ߵĸ��ߵľ�����������ߵ��д��࣮
������ͼ�٣�����ABC�У�DΪ��BC���е㣬AE��BC��E�����߶�DE�ij�������BC���д��࣮
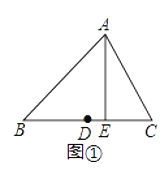
��1����������һ�ߵ��д���Ϊd��d��0������d=0����������������һ����________���ƶϵ���ѧ������________��
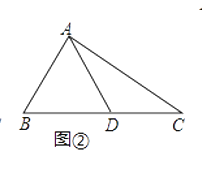
��2����ͼ�ڣ�����ABC�У���B=45����AB=![]() ��BC=8��ADΪ��BC�����ߣ����BC���д��࣮
��BC=8��ADΪ��BC�����ߣ����BC���д��࣮
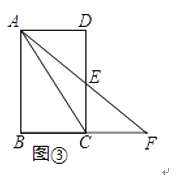
��3����ͼ�ۣ��ھ���ABCD�У�AB=6��AD=4����EΪ��CD���е㣬����AE���ӳ���BC���ӳ����ڵ�F������AC������ACF�б�AF���д��࣮
���𰸡���1�����������Σ��߶εĴ�ֱƽ�����ϵĵ㵽���˵ľ�����ȣ���2��1����3��![]() .
.
�������������������1�������߶εĴ�ֱƽ���ߵ����ʼ����жϡ�
��2����ͼ���У���AE��BC��E��������֪�ó�AE=BE�������BD�ij����������DE�ij���
��3����ͼ���У���CH��AF��H����֤��ADE�ա�FCE���ó�AE=EF�����ù��ɶ������AE�ij���Ȼ��֤����ADE�ס�CHE�������������EH���ɡ�
�⣺��1�����������Σ��߶εĴ�ֱƽ�����ϵĵ㵽���˵ľ������
��2���⣺��ͼ���У���AE��BC��E��
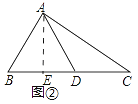
��Rt��ABE�У��ߡ�AEB=90�㣬��B=45�㣬AB=3 ![]() ��
��
��AE=BE=3��
��ADΪBC�����ߣ�BC=8��
��BD=DC=4��
��DE=BD��BE=4��3=1��
���BC���д���Ϊ1
��3���⣺��ͼ���У���CH��AF��H��
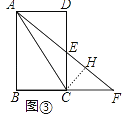
���ı���ABCD�Ǿ��Σ�
���D=��EHC=��ECF=90�㣬AD��BF��
��DE=EC����AED=��CEF��
���ADE�ա�FCE��
��AE=EF��
��Rt��ADE����AD=4��DE=3��
��AE= ![]() =5��
=5��
�ߡ�D=EHC����AED=��CEH��
���ADE�ס�CHE��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��EH= ![]() ��
��
���ACF�б�AF���д���Ϊ ![]()


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���֪AB��3��AD��8����EΪBC���е㣬����AE��EF�ǡ�AEC��ƽ���ߣ���AD�ڵ�F����FD����������

A. 3B. 4C. 5D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
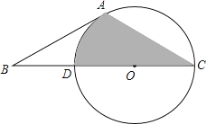
����Ŀ����ͼ����֪��O�İ뾶Ϊ4��CD�ǡ�O��ֱ����ACΪ��O���ң�BΪCD�ӳ����ϵ�һ�㣬��ABC=30�㣬��AB=AC��
��1����֤��ABΪ��O�����ߣ�
��2������AC�ij���
��3����ͼ����Ӱ���ֵ����������������У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �����ڵ�
�����ڵ�![]() ����
����![]() ����
����![]() (
(![]() ��
��![]() ��),��
��),��![]() ��
��
(1)��ͼ![]() ,�������ߵĽ���ʽ��
,�������ߵĽ���ʽ��
(2)��ͼ![]() ,�ڵ�һ����������������һ��
,�ڵ�һ����������������һ��![]() ,�ҵ�
,�ҵ�![]() �ڶԳ�����Ҳ࣬����
�ڶԳ�����Ҳ࣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() ,����
,����![]() ��
��![]() ��Ĵ���,����Ϊ
��Ĵ���,����Ϊ![]() ,���
,���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ,���
,���![]() ��
��![]() �ĺ�����ϵʽ(��Ҫ��д���Ա�����ȡֵ��Χ)��
�ĺ�����ϵʽ(��Ҫ��д���Ա�����ȡֵ��Χ)��
(3)��ͼ![]() ,��(2)�������£��ڵ�
,��(2)�������£��ڵ�![]() �Ҳ�
�Ҳ�![]() ������һ��
������һ��![]() ,��
,��![]() ,����
,����![]() ,��
,��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ,����
,����![]() ,��
,��![]() ���߶�
���߶�![]() ���ӳ�����һ��,����
���ӳ�����һ��,����![]() ,ʹ
,ʹ![]() ,ȡ
,ȡ![]() �е�
�е�![]() ,���߶�
,���߶�![]() ��ȡһ��
��ȡһ��![]() ,����
,����![]() ��
��![]() �߶��ཻ�ڵ�
�߶��ཻ�ڵ�![]() ,����
,����![]() ,���߶�
,���߶�![]() ��ȡһ��
��ȡһ��![]() ������
������![]() ��ʹ��
��ʹ��![]() ,��
,��![]() ,��
,��![]() �����
�����![]() ������.
������.



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
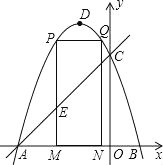
����Ŀ����ͼ��������y����x2��2x+3��ͼ����x�ύ��A��B����(��A�ڵ�B�����)����y�ύ�ڵ�C����DΪ�����ߵĶ��㣮
(1)���A��B��C�����ꣻ
(2)��M(m��0)Ϊ�߶�AB��һ��(��M�����A��B�غ�)������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N���ɵþ���PQNM����ͼ����P�ڵ�Q��ߣ����ú�m��ʽ�ӱ�ʾ����PQNM���ܳ���
(3)������PQNM���ܳ����ʱ��m��ֵ�Ƕ��٣��������ʱ�ġ�AEM�������
(4)��(3)�������£�������PMNQ���ܳ����ʱ������DQ������������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G(��G�ڵ�F���Ϸ�)����FG��2![]() DQ�����F�����꣮
DQ�����F�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ��ѧ�桢���·硢��������ѧ�������٣�ijУ��չ��־Ը�߷��������Ŀ�����䶾����������������ͨ���������ذ���������������ֲ�������������������������ڼ䣬�����ȡ�˲���ѧ����־Ը�߷���������е��飬������֣��������ÿ��ѧ���������˻�����ٵIJ�����1����IJ�����5����ݵ�������������ͼ��ʾ������������ͳ��ͼ������ͳ��ͼ��

��1���������ȡ��ѧ�����ж�������
��2��������ͳ��ͼ�У�����Ϊ3���ѧ������Ӧ������Բ�ĽǵĶ���������ȫ����ͳ��ͼ��
��3����У����ѧ��2000�ˣ��������в�����4���5����ѧ�����ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����2015��Ͷ���������2900��Ԫ��2017��Ͷ���������3509��Ԫ.
(1)��2015����2017��õ���Ͷ��������ѵ���ƽ��������;
(2)��������������涨���������ѵ�Ͷ�벻���ڹ���������ֵ�İٷ�֮�ģ���ϸõ�������������ֵ������������õ�����2019����Ͷ���������4250��Ԫ�������(1)�н�������Ͷ��������ʣ���2019��õ���Ͷ��Ľ��������Ƿ��ܴﵽ4250��Ԫ?��˵������.
(�����: ![]() ��
��![]() ��
��![]() ��
��![]() )
)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������̽������ʾ����������A��һ����¥����B�ĸ���Ϊ![]() �����ⶰ��¥�ײ�C�ĸ���Ϊ
�����ⶰ��¥�ײ�C�ĸ���Ϊ![]() ��������A�ĸ߶�Ϊ270�ף����ⶰ��¥�ĸ߶�Ϊ______��
��������A�ĸ߶�Ϊ270�ף����ⶰ��¥�ĸ߶�Ϊ______��![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
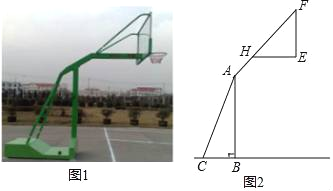
����Ŀ����ͼ1��2�ֱ���ij������ܵ�ʵ��ͼ��ʾ��ͼ����֪AB��BC�ڵ�B������BC�ij�Ϊ1�ף�����BC��֧��AC���ɵĽǡ�ACB��60������H��֧��AF�ϣ�����ײ�֧��EH��BC��EF��EH�ڵ�E����֪AH��![]() �ף�HF��
�ף�HF��![]() �ף�HE��1�ף�
�ף�HE��1�ף�
(1)������ײ�֧��HE��֧��AF���ɵĽǡ�FHE�Ķ�����
(2)������ײ���E������ľ��룮(�����������)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com