Question

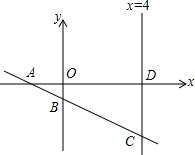
19．如图，在直标系内，一次函数y=kx+b（kb＞0，b＜0）的图象分别与x轴、y轴和直线x=4相交于A、B、C三点，直线x=4与x轴交于点D，四边形OBCD（O是坐标原点）的面积是8，若点B的纵坐标是-1．
（1）求这个一次函数解析式；
（2）E为直线CD上的一点当△ABC是以BC为腰的等腰三角形时，求出点E的坐标；
（3）若点M在x轴上运动，当M运动到某个位置时，|MB-MC|最小，试求出此时点M的坐标；
（4）若点G在直线CD上，点H在直线AB上，试问：在（3）条件下，是否存在某个合适的位置，使得MG+GH取得最小值？如果存在请直接写出这个最小值和此时点H的坐标；如果不存在请说明理由．

Answer 1

分析 （1）把点B的纵坐标是-1代入y=kx+b，得到y=kx-1，于是得到OA=-$\frac{1}{K}$，OB=1，把x=4代入得到y=4k-1，得到C（4，4k-1），根据四边形OBCD的面积是8，列方程求解；
（2）分类讨论：当BC=BE时，得到BF垂直平分CD，所以CF=EF，求得E点的坐标；当BC=CE=2$\sqrt{5}$，得到E′（4，-3-2$\sqrt{5}$），所以E的坐标是（4，1）或（4，-3-2$\sqrt{5}$）；
（3）作线段BC的中垂线交x轴于M，交BC 于N，则MB=MC，即MB-MC=0，所以点M就是符合条件的点，再根据三角形相似，列比例式求解；
（4）作点M关于直线CD的对称点M′，过点M′作M′H⊥BC于H，交CD于G，则点G，H就是符合条件的点，根据三角形相似列方程求解．

解答 解：（1）∵点B的纵坐标是-1，
∴-1=b，∴y=kx-1，
令x=0，得y=$\frac{1}{k}$，
∴OA=-$\frac{1}{K}$，OB=1，
当x=4，得到y=4k-1，
∴C（4，4k-1），
∴OD=4，CD=1-4k，
∵四边形OBCD的面积是8，
∴$\frac{1}{2}$（1+1-4k）×4=8，∴k=-$\frac{1}{2}$，
∴一次函数解析式为：y=-$\frac{1}{2}$x-1；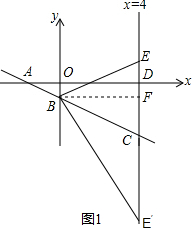

（2）如图1，当BC=BE时，过点B作BF⊥CD于F，
∵C（4，-3），
∴CD=3，
∴BC=$\sqrt{{CF}^{2}{+BF}^{2}}$=$\sqrt{{（3-1）}^{2}{+4}^{2}}$=2$\sqrt{5}$，
∴EF=CF=2，
∴E（4，1），
当BC=CE=2$\sqrt{5}$，
∴E′（4，-3-2$\sqrt{5}$），
∴点E的坐标是（4，1）或（4，-3-2$\sqrt{5}$）；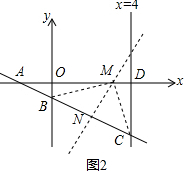

（3）如图2，作线段BC的中垂线交x轴于M，交BC 于N，
点M就是符合题意得点，即|MB-MC|最小，
∵∠DAC=∠NAM，∠ADC=∠ANM，
∴△ACD∽△AMN，
∴$\frac{AM}{AC}$=$\frac{AN}{AD}$，
∴$\frac{AM}{3\sqrt{5}}$=$\frac{2\sqrt{5}}{6}$，
∴AM=5，
∴OM=3，
∴M（3，0）；

（4）存在．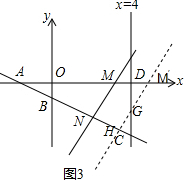
如图3，作点M关于直线CD的对称点M′，过点M′作M′H⊥BC于H，交CD于G，
则点G，H就是符合条件的点，
易证得：△ACD∽△AM′H，
∴$\frac{AD}{AH}$=$\frac{AC}{AM′}$=$\frac{CD}{HM′}$，
∴$\frac{6}{AH}$=$\frac{3}{HM′}$=$\frac{3\sqrt{5}}{7}$，
∴AH=$\frac{14\sqrt{5}}{5}$，HM′=$\frac{7\sqrt{5}}{5}$，
∴MG+GH的最小值=$\frac{7\sqrt{5}}{5}$，
∵点H在直线AB上，
∴设H（m，-$\frac{1}{2}$m-1），
∴（m+2）²${+（\frac{1}{2}m+1）}^{2}$=${（\frac{14\sqrt{5}}{5}）}^{2}$，
∴m=$\frac{18}{5}$，
∴H（$\frac{18}{5}$，-$\frac{14}{5}$）．

点评 本题考查了待定系数法求一次函数解析式，等腰三角形的判定和性质，在平面直角坐标系中求点的坐标，相似三角形的判定和性质，轴对称的性质勾股定理得应用．