
【题目】已知:如图,长方形纸片(对边平行且相等,四个角是直角)按如图方式折叠,使顶点B和点D重合,折痕为EF且AB=3cm,BC=5cm.
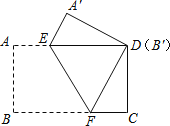
(1)求证:△DEF是等腰三角形;
(2)求:△DEF的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)根据长方形的性质得AD∥BC,则∠DEF=∠EFB,再由折叠的性质得∠EFB=∠EFD,从而得出DE=DF,即△DEF是等腰三角形;
(2)设DF=x,则FC=5﹣x,由折叠的性质可知BF=x,根据勾股定理得出x的值,即可得出S △DEF.
(1)证明∵在长方形ABCD中AD∥BC,
∴∠DEF=∠EFB,
∵折叠,
∴∠EFB=∠EFD,
∴∠DEF=∠EFD,
∴DE=DF,
∴△DEF是等腰三角形;
(2)解:设DF=x,则FC=5﹣x,
折叠可知BF=x,
在△DFC中,∠C=90°,得:
(5﹣x)2+32=x2,
DE=DE=x=![]() ,
,
∴S △DEF=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】下列说法中正确的是 ( )
A. 三角形的外角大于任何一个内角 B. 三角形的内角和小于外角和
C. 三角形的外角和小于四边形的外角和 D. 三角形的一个外角等于两个两个内角的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
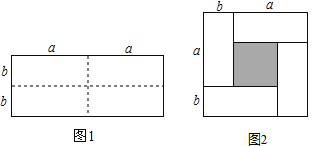
【题目】如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为 ;小正方形(阴影部分)的边长为 .(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(a﹣b)2,(a+b)2,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
(3)已知a+b=4,ab=3.求代数式a﹣b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
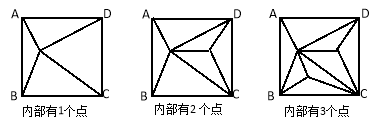
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com