
����Ŀ��ij�������Ʊ�۸������
��Ʊ����/�� | 1��50 | 51��100 | 100���� |
ÿ����Ʊ��/Ԫ | 12 | 10 | 8 |
ijУ���꼶��1������2������ƻ�ȥ�����þ��㣬���У�1������������50�ˣ���2������������50��������100�ˣ���������Ϊ��λ������Ʊ����һ��֧��1118Ԫ�������������������Ϊһ�����幺Ʊ����ֻ�軨��816Ԫ��
��1����������ж�����ѧ����
��2�����幺Ʊ�뵥����Ʊ��Ƚϣ����������Լ�˶���Ǯ��
���𰸡�
��1��
�����꼶��1������x�ˡ����꼶��2������y�ˣ������⣬��
![]() ��
��
��ã�![]()
�����꼶��1������49�ˡ����꼶��2������53�ˣ�
��2��
���꼶��1�����ʡ�ķ���Ϊ����12��8����49=196Ԫ��
���꼶��2�����ʡ�ķ���Ϊ����10��8����53=106Ԫ��
����������1�������꼶��1������x�ˡ����꼶��2������y�ˣ�������������Ϊ��λ������Ʊ����һ��֧��1118Ԫ�������������������Ϊһ�����幺Ʊ����ֻ�軨��816Ԫ���������������⼴�ɣ�
��2����һ��Ʊ��ʡ�ķ��á��ð�����������⣮


 �ƸԹھ��ο���ϵ�д�
�ƸԹھ��ο���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ��ѡ��ѧ���μӡ�������д���������Ծ��꼶һ�ࡢ�����10��ѧ�����к�����д���ԣ��Ʒֲ���10���ƣ��÷־�ȡ���������ɼ��ﵽ6�ֻ�6������Ϊ���õ�9��Ϊ���㣬�ɼ����1��ʾ���������˳ɼ�����������2����
��1
һ�� | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
���� | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
��2
�༶ | ƽ���� | ��λ�� | ���� | ���� | ������ | ������ |
һ�� | 7.6 | 8 | a | 3.82 | 70% | 30% |
���� | b | 7.5 | 10 | 4.94 | 80% | 40% |
��1���ڱ�2�У�a= ��b= ��
��2������˵����ļ����ʡ������ʾ�����һ�࣬���Զ����һ��ã���Ҳ������Ϊһ��ɼ��ȶ���ã�����������һ��ɼ��õ��������ɣ�
��3��һ�ࡢ��������ֵ���ͬѧ�Ա�ֱ���1��1Ů��2��1Ů���ִ�����������ֵ�ͬѧ�и���1��ͬѧ�μӡ�������д������������״ͼ���б������ǡ�ó鵽1��1Ů��λͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����25��ѧ����ѧ����ɼ�����λ���֣���Ƶ���ֲ�ֱ��ͼ��ͼ��
��1���ɼ�x��ʲô��Χ��������ࣿ�Ƕ����ˣ�
��2�����ð뾶Ϊ2������ͼ���������ɼ���60��x��70��������Ӧ����������Ƕ��٣�
��3������ɼ���50��x��60��90��x��100��ѧ������ѡ2�ˣ�С��ɼ���96�֣�����״ͼ���б����г����п��ܽ������С�ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ˮƽ����һ�����ǰ��һ�������������ǰ�ı�AB����������ֱ��DE��һ��ֱ���ϣ�AB=BC=6cm��OD=3cm����ʼ��ʱ��BD=1cm���������ǰ���2cm/s���ٶ������ƶ���
��1����B��O�غϵ�ʱ�������ǰ��˶���ʱ�䣻
��2����ͼ2����AC���Բ����ʱ����AD��
��3����ͼ3����AB��DE�غ�ʱ����֤��CF2=CGCE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y=![]() ��ͼ���һ֧λ�ڵ�һ���ޣ�
��ͼ���һ֧λ�ڵ�һ���ޣ�
��1���жϸú���ͼ�����һ֧���ڵ����ޣ�����m��ȡֵ��Χ��
��2����ͼ��OΪ����ԭ�㣬��A�ڸ÷���������λ�ڵ�һ����ͼ���ϣ���B���A����x��Գƣ�����OAB�����Ϊ6����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ˮ�к�����д�����У�10��ѧ���÷�������
���� | 3 | 4 | 2 | 1 |
���� | 80 | 85 | 90 | 95 |
��ô��10��ѧ�����÷�������λ���������ֱ��ǣ�������
A.85��82.5
B.85.5��85
C.85��85
D.85.5��80
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㵺���ҹ�����������ijУ���꼶��15������С�����������Ϊ������ʱ�����йص��㵺���ŵĻ�ȡ;�����Ա���50��ѧ�����е��飨Ҫ��ÿλͬѧ��ֻѡ�Լ����Ͽɵ�һ�����������ͼ��ʾ������ͳ��ͼ��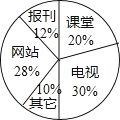
��1���ð�ѧ��ѡ���������� �ˣ�������ͳ��ͼ�У����������������������Բ�Ľ��� �ȣ���ֱ��������
��2�������У���꼶��1500��ѧ����������������ѡ����վ�������꼶ѧ��Լ�� �ˣ���ֱ��������
��3��������꼶��15�����ί�����5�ֻ�ȡ;������ѡ���ֶ�ȫУѧ�����е��飬��ǡ��ѡ�á���վ���͡����á��ĸ��ʣ�������״ͼ���б����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������max{a��b}����a��bʱ��max{a��b}=a����a��bʱ��max{a��b}=b����max{��3��2}=2��
��1��max{![]() ��3}= ��
��3}= ��
��2����֪y1=![]() ��y2=k2x+b��ͬһ����ϵ�е�ͼ����ͼ��ʾ����max{
��y2=k2x+b��ͬһ����ϵ�е�ͼ����ͼ��ʾ����max{![]() ��k2x+b}=
��k2x+b}=![]() �����ͼ��ֱ��д��x��ȡֵ��Χ��
�����ͼ��ֱ��д��x��ȡֵ��Χ��
��3���÷������۵ķ�������max{2x+1��x��2}��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ڻ��زμ����ʵ�������У�������ʦ����ѧ�������ؼƻ��½�һ�����ε������أ�һ�߿���ǽ��ǽ�㹻�����������������ܳ�69�IJ����դ��Χ�ɣ���ǽƽ�е�һ����һ����Ϊ3�ij���ڣ���ͼ��ʾ�������Ʋ���ʹ�صĶ��������������λѧ��������龳��
������������Ϣ��������⣺
��1����AB=x�ף�x��0�������ú�x�Ĵ���ʽ��ʾBC�ij�
��2�������ж�˭��˵����ȷ��Ϊʲô��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com