
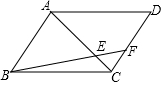
 如图,在?ABCD中,点F在CD上,且CF:DF=1:2,则S△CEF:S?ABCD=1:24.
如图,在?ABCD中,点F在CD上,且CF:DF=1:2,则S△CEF:S?ABCD=1:24. 分析 设CF=a,DF=2a,S△CEF=S,则CD=3a.利用相似三角形的性质求出平行四边形的面积,即可解决问题.
解答 解:设CF=a,DF=2a,S△CEF=S,则CD=3a.
∵四边形ABCD是平行四边形,
∴AB=CD=3a,AB∥CF,
∴△CFE∽△ABE,
∴$\frac{CF}{AB}$=$\frac{CE}{AE}$=$\frac{1}{3}$,
∴$\frac{{S}_{△EFC}}{{S}_{△ABE}}$=$\frac{1}{9}$,
∴S△ABE=9S,
∴S△BCE=3S,
∴S平行四边形ABCD=2•S△ABC=24S,
∴S△CEF:S?ABCD=1:24,
故答案为1:24.
点评 本题考查平行四边形的性质、相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{7b}{3a}$ | B. | $\frac{7b}{3ac}$ | C. | $\frac{3a}{7b}$ | D. | $\frac{3ac}{7b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正有理数和负有理数统称为有理数 | |
| B. | 符号不同的两个数互为相反数 | |
| C. | 绝对值等于它的相反数的数是非正数 | |
| D. | 两数相加,和一定大于任何一个加数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,点A(0,2),B(6,4).
在平面直角坐标系中,点A(0,2),B(6,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-14)-(+5)=-9 | B. | 0-(-3)=0+(-3) | C. | (-3)×(-3)=-6 | D. | (-18)÷(-$\frac{2}{3}$)=27 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com