
分析 首先根据直线上的点的坐标与直线解析式的关系求出A、B两点的坐标,可设点C的坐标为(x,3x+3),由点到直线的距离公式求出点C到直线AB的距离,然后根据三角形的面积为8列方程求解即可.
解答 解:∵点A(a,a+3)在直线函数y=2x+1上,
∴2a+1=a+3,
∴a=2,
∴A、B两点的坐标分别为:A(2,5),B(-$\frac{7}{2}$,-6).
∵在直线y=3x+3上存在一点C,使得ABC的面积为8,设点C的坐标为(x,3x+3),
∴点C到直线AB的距离为:$\frac{|2x-(3x+3)+1|}{\sqrt{{2}^{2}+{1}^{2}}}$=$\frac{|-x-2|}{\sqrt{5}}$
又∵ABC的面积为8,且AB=$\sqrt{(2+\frac{7}{2})^{2}+(5+6)^{2}}$=$\frac{11}{2}\sqrt{5}$
∴$\frac{1}{2}$×$\frac{11}{2}\sqrt{5}$×$\frac{|-x-2|}{\sqrt{5}}$=8,
解之得:x1=$\frac{10}{11}$,x2=-$\frac{54}{11}$
所以符合要求的点C的坐标为:($\frac{10}{11}$,$\frac{63}{11}$)或(-$\frac{54}{11}$,-$\frac{119}{11}$).
点评 本题考查了一次函数图象上的点的坐标特征问题,解题的关键是求点到直线的距离.


科目:初中数学 来源: 题型:填空题
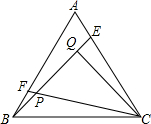 如图所示,点E、F分别是正△ABC的边AC、AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE=7.
如图所示,点E、F分别是正△ABC的边AC、AB上的点,AE=BF,BE,CF相交于点P,CQ⊥BE于Q,若PF=1,PQ=3,则BE=7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,点D,E分别在AB,AC上,若$\frac{AD}{DB}$=$\frac{AE}{EC}$,且AE=2,EC=4,DB=5,求AB的长.
如图,在△ABC中,点D,E分别在AB,AC上,若$\frac{AD}{DB}$=$\frac{AE}{EC}$,且AE=2,EC=4,DB=5,求AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com