
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�O������ԭ�㣬������OACB�Ķ���A��B�ֱ���x����y���ϣ���֪OA=3��OB=5����DΪy����һ�㣬������Ϊ��0��1������P�ӵ�A������ÿ��1����λ���ٶ����߶�AC��CB�ķ����˶�������P���B�غ�ʱֹͣ�˶����˶�ʱ��Ϊt�룮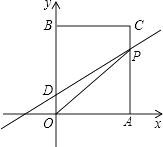
��1������P������Cʱ����ֱ��DP�ĺ�������ʽ��
��2�������OPD�����S����t�ĺ�������ʽ��
�ڵ���D����OP�ĶԳƵ�����x����ʱ�����P�����꣮
��3����P���˶��������Ƿ����ʹ��BDPΪ���������Σ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺���ʱֱ��DP����ʽΪy=kx+b��
��D��0��1����C��3��5������ã� ![]() ��
��
��ã� ![]() ��
��
���ʱֱ��DP����ʽΪy= ![]() x+1
x+1
��2��
�⣺�ٵ���P���߶�AC��ʱ��OD=1����Ϊ3��S= ![]() ��
��
����P���߶�BC��ʱ��OD=1����Ϊ3+5��t=8��t��S= ![]() ��1����8��t��=��
��1����8��t��=�� ![]() t+4��
t+4��
�ڵ���D����OP�ĶԳƵ�����x����ʱ��D�ԳƵ�Ϊ��1��0������ʱֱ��OPΪy=x��
���ʱ��P�������ǣ�3��3��
��3��
�⣺���ڣ�����Ϊ��
����BDPΪ���������Σ�������������ǣ�
�ٵ�BD=BP1=OB��OD=5��1=4��
��Rt��BCP1��BD=4��BC=3��
���ݹ��ɶ����ã�CP1= ![]() =
= ![]() ��
��
��AP1=5�� ![]() ����P1��3��5��
����P1��3��5�� ![]() ����
����
�ڵ�BP2=DP2ʱ����ʱP2��3��3����
�۵�DB=DP3=4ʱ��
��Rt��DEP3��DE=3��
���ݹ��ɶ����ã�P3E= ![]() =
= ![]() ��
��
��AP3=AE+EP3= ![]() +1����P3��3��
+1����P3��3�� ![]() +1����
+1����
���ϣ����������P����Ϊ��3��3����3�� ![]() +1����3��5��
+1����3��5�� ![]() ����
����
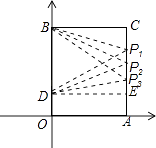
����������1����ֱ��DP����ʽΪy=kx+b����D��B����������k��b��ֵ������ȷ��������ʽ����2���ٵ�P��AC��ʱ��������ODP��OD���Ϊ�̶�ֵ�������ʱ�������P��BC��ʱ���ױ�ODΪ�̶�ֵ����ʾ���ߣ������г�S��t�Ĺ�ϵʽ���ڵ�D����OP�ĶԳƵ�����x����ʱ��ֱ��OPΪy=x�������ʱP���꼴�ɣ���3�����ڣ��ֱ���BD��DP��BPΪ�ױ�����������ǣ����ù��ɶ�����ͼ���������������P���꼴�ɣ�
�����㾫����������Ҫ������һ�κ��������ʺ�һ�κ�����ͼ������ʵ����֪ʶ�㣬��Ҫ����һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С��һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ������ȷ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
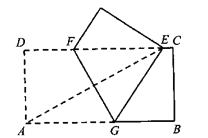
����Ŀ����ͼ������ֽƬABCD�У�AD= 1,ABһ2.��ֽƬ�۵���ʹ����A���CD�ϵĵ�E�غϣ��ۺ�FG�ֱ���AB��CD���ڵ�G��F,AE��FG���ڵ��ǵ���ED�����Բ��BC������BC���е�N.���ۺ�FG�ij�Ϊ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ� �����֪x��y=2����x��1��y��0����ȷ��x+y��ȡֵ��Χ�������½ⷨ��
�⣺��x��y=2���֡�x��1����y+2��1����y����1
��y��0���ੁ1��y��0������
ͬ���ã�1��x��2������
�ɢ�+�ڵé�1+1��y+x��0+2����x+y��ȡֵ��Χ��0��x+y��2��
�밴����������������������⣺
��֪����x��y�ķ����� ![]() �ĽⶼΪ�Ǹ�����
�ĽⶼΪ�Ǹ�����
��1����a��ȡֵ��Χ��
��2����֪2a��b=1���ң���a+b��ȡֵ��Χ��
��3����֪a��b=m��m�Ǵ���1�ij���������b��1����2a+b���ֵ�����ú�m�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ��ʡij��ij�������¶�Ϊ��7�棬����ҹ�²�Ϊ12�棬������¶�Ϊ�� ��
A.5��
B.7��
C.��12��
D.��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������3��4��x��6��8��ƽ������5�����������ݵ������ǣ� ��
A.3B.4C.6D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
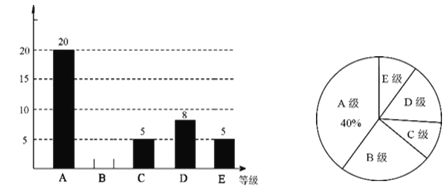
����Ŀ��Ϊ��ǿ��ͬѧ�ǵ�У��ȫ��ʶ��ijѧУ��֯ȫУ3000��ͬѧ�μ�У��ȫ֪ʶ���ԣ��ɼ���ΪA��B��C��D��E��5���ȼ���Ϊ�˽Ȿ�β��Եijɼ����ȼ���������ִ��������ȡ����ͬѧ�ijɼ����ȼ�����ͳ�����������������µ�ͳ��ͼ��
��1����������������������� ��
��2���벹ȫ����ͳ��ͼ��
��3��������Գɼ����ȼ���ΪA��B��C���Ķ�Ϊ���㣬����Ƹ�ѧУ�μӱ���У��ȫ֪ʶ���Գɼ����ȼ����ﵽ�����ͬѧ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е����У����õĵ��鷽ʽ�����˵��ǣ� ��
A. �˽�������ѧ���Ľ�ˮ��ʶ��ȡ��������ķ�ʽ
B. Ϊ�˵���һ��ʡ�Ļ�����Ⱦ����������ʡ��ʡ�����
C. �˽���ڶ�һ����Ӱ�������������������Ϊ�����ŵ�����
D. �˽����Ա�����Ĵ���ʲ�ȡ�ղ鷽ʽ
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com