
【题目】如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.

【答案】(1)证明见解析;(2)S△ABE=![]() .
.
【解析】
(1)由四边形ABCD是矩形与折叠性质,易得AB=AG,∠BAE=∠GAF,∠BEA=∠EAF=∠GFA,则可利用AAS判定:△ABE≌△AGF;
(2)据折叠的性质可得AE=EC,在直角△ABE中,根据勾股定理可列方程求得BE的长,再根据三角形的面积公式计算即可.
(1)∵四边形ABCD是矩形,
∴AB=CD,∠BAD=∠BCD,
由折叠的性质得:AG=CD,∠EAG=∠BCD,
∴AB=AG,∠BAD=∠EAG,
∴∠BAE=∠GAF,
又∵AB∥CD,AE∥GF,AD∥BC,
∴∠BEA=∠EAF=∠GFA,
在△ABE和△AGF中,
∠BEA=∠GFA
∠BAE=∠GAF
AB=AG,
∴△ABE≌△AGF(AAS);
(2)根据折叠的性质可得AE=EC,
设BE=x,则AE=EC=8-x,
在直角△ABE中,根据勾股定理可得62+x2=(8-x)2,
解得:x=![]() ,
,
则S△ABE=![]() ABBE=
ABBE=![]() ×6×
×6×![]() =
=![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,BM是∠ABC的平分线,交CD于点M,且DM=2,平行四边形ABCD的周长是14,则BC的长等于( )
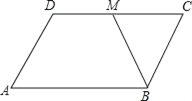
A. 2B. 2.5C. 3D. 3.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,点A、O、B依次在直线MN上,现将射线OA绕点O沿顺时针方向以每秒2°的速度旋转,同时射线OB绕点O沿逆时针方向以每秒4°的速度旋转,如图2,设旋转时间为t(0秒≤t≤90秒).
(1)用含t的代数式表示∠MOA的度数.
(2)在运动过程中,当∠AOB第二次达到60°时,求t的值.
(3)在旋转过程中是否存在这样的t,使得射线OB是由射线OM、射线OA、射线ON中的其中两条组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请直接写出t的值;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
如图1,在四边形ABCD的边AB上任取一点E(点E不与点A、点B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.
解决问题:
(1)如图1,∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB和BC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
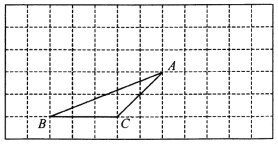
【题目】如图,方格纸中每个小正方形的边长为1个单位长度,三角形ABC的顶点都在格点上,将三角形ABC向右平移2个单位长度,再向上平移3个单位长度,得到三角形A′B′C′
(1)请在图中画出三角形A′B′C′;
(2)求三角形ABC的面积;
(3)若AC的长约为2.8,则边AC上的高约为多少?(结果保留分数)
查看答案和解析>>
科目:初中数学 来源: 题型:
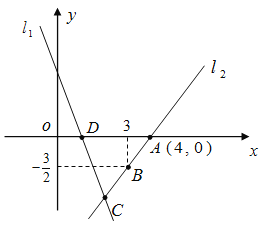
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() 、
、![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)求![]() 的面积;
的面积;
(4)在直线![]() 上存在异于点
上存在异于点![]() 的另一个点
的另一个点![]() ,使得
,使得![]() 与
与![]() 的面积相等,求
的面积相等,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com