
【题目】在平面直角坐标系中,△DEF是△ABC经过某种变换得到的图形,点A与点D,点B与点F,点C与点E分别是对应点(如图所示),观察对应点与点的坐标之间的关系,解答下列问题:

(1)分别写出点A与点D,点B与点F,点C与点E的坐标
(2)若点P(a+9,4﹣b)与点Q(2a,2b﹣3)也是通过上述变换得到的对应点,求a、b的值.
【答案】(1)(1)点A的坐标为(2,3),点D的坐标为(﹣2,﹣3),点B的坐标为(4,2),点F的坐标为(﹣4,﹣2),点C的坐标为(1,1),点E的坐标为(﹣1,﹣1);
(2)a=﹣3,b=﹣1.
【解析】
试题分析:(1)根据坐标与图形的性质写出各点的坐标;
(2)找出对应点的横纵坐标之间的关系,列式计算即可.
解:(1)点A的坐标为(2,3),点D的坐标为(﹣2,﹣3),点B的坐标为(4,2),点F的坐标为(﹣4,﹣2),点C的坐标为(1,1),点E的坐标为(﹣1,﹣1);
(2)由对应点的坐标可知,对应点的横、纵坐标互为相反数,
∴a+9+2a=0,4﹣b+2b﹣3=0,
解得,a=﹣3,b=﹣1.


科目:初中数学 来源: 题型:
【题目】在信宜市某“三华李”种植基地有A、B两个品种的树苗出售,已知A种比B种每株多2元,买1株A种树苗和2株B种树苗共需20元.
(1)问A、B两种树苗每株分别是多少元?
(2)为扩大种植,某农户准备购买A、B两种树苗共360株,且A种树苗数量不少于B种数量的一半,请求出费用最省的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分.已知抛物线的对称轴为x=2,与x轴的一个交点是(﹣1,0).有下列结论:
①abc>0;②4a﹣2b+c<0;③4a+b=0;④抛物线与x轴的另一个交点是(5,0);⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1<y2.
其中正确的是( )

A.①②③ B.②④⑤ C.①③④ D.③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的BC边上的一点,AD=BD,∠ADC=80°.
(1)求∠B的度数;
(2)若∠BAC=70°,判断△ABC的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
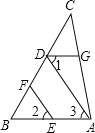
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.
解:∵EF∥AD(已知)
∴∠2=∠3 )---①
又∵∠1=∠2(已知)
∴∠1=∠3( )----②
∴AB∥______( )----③
∴∠BAC+∠AGD=180°( )----④
∵∠BAC=70°(已知)
∴∠AGD=1800-700=1100
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com