练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，D是△ABC的BC边上的一点，AD=BD，∠ADC=80°．

    （1）求∠B的度数；

    （2）若∠BAC=70°，判断△ABC的形状，并说明理由．

    【答案】（1）40°；（2）△ABC是等腰三角形．证明见解析.

    【解析】试题分析：（1）由由三角形外角的性质，可求得∠BAD的度数，根据等角对等边，可得AD=BD；

    （2）由∠BAC=70°，易求得∠C=∠BAC=70°，根据等角对等边的性质，可证得△ABC是等腰三角形．

    （1）∵∠ADC=∠B+∠BAD，而∠ADC=80°，∠B =40°，

    ∴∠BAD=80°-40°=40°，

    ∴∠B=∠BAD，

    ∴AD=BD.

    （2）△ABC是等腰三角形．

    理由：∵∠B=40°，∠BAC=70°，

    ∴∠C=180°﹣∠B﹣∠BAC=70°，

    ∴∠C=∠BAC，

    ∴BA=BC，

    ∴△ABC是等腰三角形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某气球内充满了一定质量的气球，当温度不变时，气球内气球的压力p（千帕）是气球的体积V（米2）的反比例函数，其图象如图所示（千帕是一种压强单位）

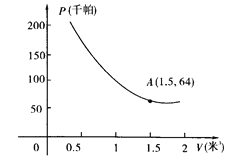
    （1）、写出这个函数的解析式；

    （2）、当气球的体积为0.8立方米时，气球内的气压是多少千帕；

    （3）、当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，△DEF是△ABC经过某种变换得到的图形，点A与点D，点B与点F，点C与点E分别是对应点（如图所示），观察对应点与点的坐标之间的关系，解答下列问题：

    （1）分别写出点A与点D，点B与点F，点C与点E的坐标

    （2）若点P（a+9，4﹣b）与点Q（2a，2b﹣3）也是通过上述变换得到的对应点，求a、b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算正确的是（ ）

    A. 3a 2 2a 6a 2 B. a 2 3 a 6 C. a 4 a 2 2 D. a 12 a 2 1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某小区准备新建50个停车位，以解决小区停车难的问题．已知新建1个地上停车位和1个地下停车位共需0.5万元；新建3个地上停车位和2个地下停车位共需1.1万元．

    （1）该小区新建1个地上停车位和1个地下停车位各需多少万元？

    （2）若该小区预计投资金额超过10万元，且地上的停车位要求不少于30个，问共有几种建造方案？

    （3）对（2）中的几种建造方案中，哪一个方案的投资最少？并求出最少投资金额．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果汽车向南行驶30米记作+30米，那么-50米表示（ ）

    A. 向东行驶50米 B. 向西行驶50米 C. 向南行驶50米 D. 向北行驶50米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，三角形ABC在直角坐标系中，

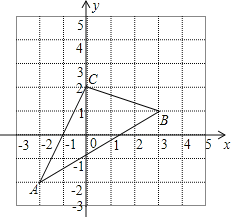
    （1）若把△ABC向上平移2个单位，再向左平移1个单位得到△A′B′C′，请在图中画出平移后图形．

    （2）请写出△A′B′C′各点的坐标．

    （3）求出三角形ABC的面积．_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“把弯曲的公路改直，就能缩短路程”，其中蕴含的数学道理是（　　）

    A. 两点确定一条直线 B. 直线比曲线短

    C. 两点之间直线最短 D. 两点之间线段最短

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一矩形纸片OABC放在平面直角坐标系中，O（0，0），A（6，0），C（0，3）．动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动，运动秒时，动点P从点A出发以相等的速度沿AO向终点O运动．当其中一点到达终点时，另一点也停止运动．设点P的运动时间为t（秒）．

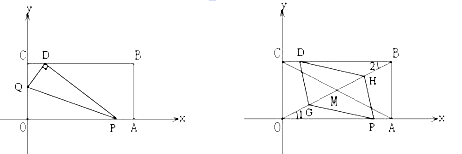
    （1）求点B的坐标，并用含t的代数式表示OP，OQ；

    （2）当t=1时，如图1，将△OPQ沿PQ翻折，点O恰好落在CB边上的点D处，求点D的坐标；

    （3）在（2）的条件下，矩形对角线AC,BO交于M,取OM中点G,BM中点H，求证当t=1时四边形DGPH是平行四边形．

    查看答案和解析>>

    同步练习册答案