
����Ŀ����һ����ֽƬOABC����ƽ��ֱ������ϵ�У�O��0��0����A��6��0����C��0��3��������Q�ӵ�O������ÿ��1����λ�����ٶ���OC���յ�C�˶����˶�![]() ��ʱ������P�ӵ�A��������ȵ��ٶ���AO���յ�O�˶���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������P���˶�ʱ��Ϊt���룩��
��ʱ������P�ӵ�A��������ȵ��ٶ���AO���յ�O�˶���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������P���˶�ʱ��Ϊt���룩��
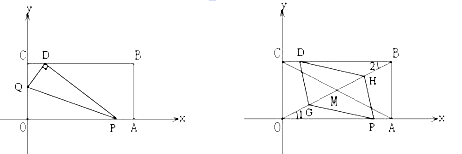
��1�����B�����꣬���ú�t�Ĵ���ʽ��ʾOP��OQ��
��2����t=1ʱ����ͼ1������OPQ��PQ���ۣ���Oǡ������CB���ϵĵ�D�������D�����ꣻ
��3���ڣ�2���������£����ζԽ���AC,BO����M,ȡOM�е�G,BM�е�H����֤��t=1ʱ�ı���DGPH��ƽ���ı�����
���𰸡���1��B��6,3����OP=6��t��OQ=![]() +t����2��D��1,3������3��֤�����̼�����
+t����2��D��1,3������3��֤�����̼�����
��������
�����������1�����ݾ��ε����������B�����꣬���ݶ����������OP��OQ�ij��ȣ���2�������۵�ͼ�ε��������OQ��DQ�ij��ȣ�Ȼ����ݹ��ɶ������CD�ij��ȣ��õ���D�����ꣻ��3������һ��Ա�ƽ������ȵ��ı���Ϊƽ���ı��ν����ж���
�����������1��B��6,3����OP=OA-AP=6-t, OQ=![]() +t��
+t��
��2����t=1ʱ��OP=5��OQ=![]() ,��CQ=3-
,��CQ=3-![]() =
=![]() ��
��
���۵���֪����OPQ�ա�DPQ,
��OQ=DQ=![]()
�ɹ��ɶ���,�ã�CD=1
��D��1,3��
��3�����ı���OABC�Ǿ��Σ�
��OA=BC,
����CD=AP=1��
��BC-CD=OA-AP,��BD=OP,
��OM=MB,GΪOM�е㣬HΪBM�е� ,
��OG=BH,
��OA��BC
���1=��2
����POG����DBH��OG=BH����1=��2��OP=DB
���POG�ա�DBH
���OGP=��BHD��PG=DH
���MGP=��DHM
��PG��DH
����PG=DH
���ı���DGPH��ƽ���ı�����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D����ABC��BC���ϵ�һ�㣬AD=BD����ADC=80�㣮
��1�����B�Ķ�����
��2������BAC=70�����ж���ABC����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��EF��AD����1=��2����BAC=70�㣬����AGD�Ķ������뽫���������д������
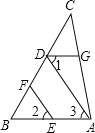
�⣺��EF��AD����֪��
���2=��3�� ����---��
���ߡ�1=��2����֪��
���1=��3���� ����----��
��AB��______���� ����----��
���BAC+��AGD=180�㣨���� ��----��
�ߡ�BAC=70�㣨��֪��
���AGD=1800-700=1100
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ͼ�������ó�����ȵ�Сľ������һ������ƴ�Ҷ��ɣ���һ��ͼ����4��Сľ�������6��ͼ��Сľ�������ǣ� ��
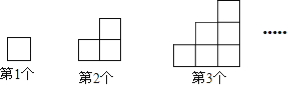
A. 42 B. 48 C. 54 D. 56
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У������������ϸ���������궼��ȥ3�������걣�ֲ��䣬������ͼ����ԭͼ�εĻ�����( )
A. ����ƽ����3����λ���� B. ����ƽ����3����λ����
C. ����ƽ����3����λ���� D. ����ƽ����3����λ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��lΪx+y=8����P��x��y����l����x��0��y��0����A������Ϊ��6��0����
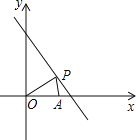
��1������OPA�����ΪS����S��x�ĺ�����ϵʽ����ֱ��д��x��ȡֵ��Χ��
��2����S=9ʱ�����P�����ꣻ
��3����ֱ��l����һ��M��ʹOM+MA�ĺ���С�����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪P=210��3��58 �� ��P���ÿ�ѧ��������ʾΪ�� ��
A.12��108
B.1.2��109
C.1.2��108
D.12��109
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com