
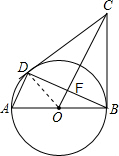
 如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO.
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上的一点,且AD∥CO.| 2 |
|
| 2 |
| OB2+BC2 |
| 3 |
| AD |
| OB |
| AB |
| OC |
| AD |
| 1 |
| 2 | ||
|
2
| ||
| 3 |


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
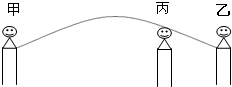 自从我市实行大课间活动以来,跳大绳成了同学们最喜爱的活动方式,你知道吗?在我们跳大绳时,绳甩到最高处的形状可近似地看为抛物线,如图,正在甩绳的甲、乙两名同学拿绳的手间距离均为4米,手距地面均为1米,同学丙直立在距甲拿绳的手水平距离3米处,其身高为1.5米,当绳子甩到最高处时刚好通过他的头顶(假设在跳绳过程中人的顶部与地面的距离不变).
自从我市实行大课间活动以来,跳大绳成了同学们最喜爱的活动方式,你知道吗?在我们跳大绳时,绳甩到最高处的形状可近似地看为抛物线,如图,正在甩绳的甲、乙两名同学拿绳的手间距离均为4米,手距地面均为1米,同学丙直立在距甲拿绳的手水平距离3米处,其身高为1.5米,当绳子甩到最高处时刚好通过他的头顶(假设在跳绳过程中人的顶部与地面的距离不变).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com