
 MN折叠,使MB与DN交于点K,得到△MNK,则对△MNK的叙述正确的个数是:
MN折叠,使MB与DN交于点K,得到△MNK,则对△MNK的叙述正确的个数是: ①如图,∵四边形ABCD是矩形,
①如图,∵四边形ABCD是矩形, ×3×3=4.5,故此选项正确;
×3×3=4.5,故此选项正确;
 -4×3×
-4×3× =7.5.
=7.5.  ×9×3-
×9×3- ×4×3=7.5,故此选项正确;
×4×3=7.5,故此选项正确;

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
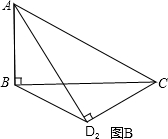
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4| 3 |
| 3 |


查看答案和解析>>
科目:初中数学 来源: 题型:
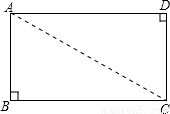
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(37):2.7 最大面积是多少(解析版) 题型:解答题
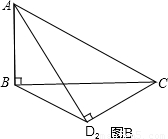
 ,将矩形沿对角线AC剪开,解答以下问题:
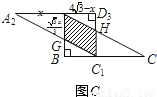
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



查看答案和解析>>
科目:初中数学 来源:第25章《图形的变换》中考题集(30):25.3 轴对称变换(解析版) 题型:解答题
 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



查看答案和解析>>
科目:初中数学 来源:2007年全国中考数学试题汇编《二次函数》(06)(解析版) 题型:解答题
 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: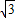 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.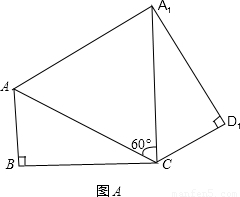
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com