
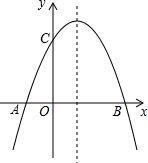
 抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0)、B(3,0)两点.
抛物线y=ax2+bx+2(a≠0)与x轴交于A(-1,0)、B(3,0)两点.分析 (1)把A(-1,0)、B(3,0)两点坐标代入y=ax2+bx+2(a≠0),得$\left\{\begin{array}{l}a-b+2=0\\ 9a+3b+2=0\end{array}\right.$,求出a,b的值,即可解答.
(2)点D的坐标为(1,m),当∠ODB=90°时,根据勾股定理求出m的值,所以当∠ODB为锐角时,m的取值值范围为:m>$\sqrt{2}$或m$<-\sqrt{2}$.
(3)由题知E(n,0)、F(n,$-\frac{2}{3}{n^2}+\frac{4}{3}n+2$),分两种情况讨论:当n<-1时,当-1<n<3时,由△BEF∽△COB,得到$\frac{EF}{OB}=\frac{BE}{CO}$,进一步得到关于n的方程,即可求出n的值.
解答 解:(1)把A(-1,0)、B(3,0)两点坐标代入y=ax2+bx+2(a≠0),
得$\left\{\begin{array}{l}a-b+2=0\\ 9a+3b+2=0\end{array}\right.$
解得:$\left\{\begin{array}{l}a=-\frac{2}{3}\\ b=\frac{4}{3}\end{array}\right.$,
抛物线的解析式$y=-\frac{2}{3}{x^2}+\frac{4}{3}x+2$.
(2)如图1,当∠ODB=90°时,
∵抛物线的解析式$y=-\frac{2}{3}{x^2}+\frac{4}{3}x+2$.
∴抛物线的对称轴为x=1,
∵D点的纵坐标为m,
∴点D的坐标为(1,m),
在Rt△DEO中,OD2=OE2+DE2=12+m2=1+m2,
在Rt△DEB中,DB2=DE2+BE2=m2+22=m2+4,
在Rt△ODB中,OB2=OD2+BD2
即32=1+m2+m2+4,
解得:m=$±\sqrt{2}$,
∴当∠ODB为锐角时,m的取值值范围为:m>$\sqrt{2}$或m$<-\sqrt{2}$.
故答案为:$m<-\sqrt{2}$或$m>\sqrt{2}$.
(3)由题知E(n,0)、F(n,$-\frac{2}{3}{n^2}+\frac{4}{3}n+2$),
当n<-1时,如图2,
由△BEF∽△COB,$\frac{EF}{OB}=\frac{BE}{CO}$,
即$\frac{{-(-\frac{2}{3}{n^2}+\frac{4}{3}n+2)}}{3}=\frac{3-n}{2}$,
整理得:4n2+n-39=0,
解得,${n_1}=-\frac{13}{4},{n_2}=3$(舍去),
当-1<n<3时,如图3,
由△BEF∽△COB,$\frac{EF}{OB}=\frac{BE}{CO}$,
即$\frac{{(-\frac{2}{3}{n^2}+\frac{4}{3}n+2)}}{3}=\frac{3-n}{2}$,
整理得:4n2-17n+15=0,
解得,${n_1}=\frac{5}{4},{n_2}=3$(舍去),
综上,当n的值等于$-\frac{13}{4}$、$\frac{5}{4}$时,△BEF∽△COB.
点评 本题考查了求二次函数的解析式、勾股定理、相似三角形的性质定理,解决本题(3)的关键是进行分类讨论,利用相似三角形的性质定理得到关于n的方程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合,
如图,矩形ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在平行四边形ABCD中,∠A=90°,AB=6cm,BC=12cm,点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,如果动点E、F同时从A、B两点出发,连接EF,若设运动时间为ts,解答下列问题.
如图所示,在平行四边形ABCD中,∠A=90°,AB=6cm,BC=12cm,点E由点A出发沿AB方向向点B匀速移动,速度为1cm/s,点F由点B出发沿BC方向向点C匀速移动,速度为2cm/s,如果动点E、F同时从A、B两点出发,连接EF,若设运动时间为ts,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
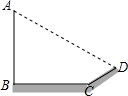 如图,某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上,量的CD=8米,BC=20米,斜坡CD的坡度比为1:$\sqrt{3}$,且此时测得1米杆的影长为2米,则电线杆的高度为( )
如图,某天小明发现阳光下电线杆AB的影子落在土坡的坡面CD和地面BC上,量的CD=8米,BC=20米,斜坡CD的坡度比为1:$\sqrt{3}$,且此时测得1米杆的影长为2米,则电线杆的高度为( )| A. | (14+2$\sqrt{3}$)米 | B. | 28米 | C. | (7+$\sqrt{3}$)米 | D. | 9米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com